Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

log_((1)/(3))81=

log⁡1381= \log _{\frac{1}{3}} 81=

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Evaluate logarithms using propertiesright chevron icon

Full solution

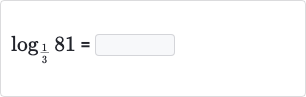
Q. log⁡1381= \log _{\frac{1}{3}} 81=
  1. Identify base and argument: Identify the base and the argument of the logarithm.\newlineThe base of the logarithm is 13\frac{1}{3} and the argument is 8181.
  2. Express as power of base: Express 8181 as a power of (1)/(3)(1)/(3).\newlineWe know that 8181 is 343^4, so we can write 8181 as ((1)/(3))−4((1)/(3))^{-4}.
  3. Rewrite logarithm with power of base: Rewrite the logarithm using the argument expressed as a power of the base. \newlinelog⁡1381\log_{\frac{1}{3}} 81 becomes log⁡13(13)−4\log_{\frac{1}{3}}\left(\frac{1}{3}\right)^{-4}.
  4. Apply property of logarithms: Apply the property of logarithms that log⁡b(bx)=x\log_b(b^x) = x. Since the base of the logarithm and the base of the exponent are the same, we can simplify the expression to −4-4.

More problems from Evaluate logarithms using properties

Question
Evaluate.\newline56÷94= \frac{5}{6} \div \frac{9}{4}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate.\newline83÷53= \frac{8}{3} \div \frac{5}{3}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate.\newline54÷35= \frac{5}{4} \div \frac{3}{5}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Evaluate.\newline34÷34= \frac{3}{4} \div \frac{3}{4}=
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the expression in exponential form.\newline6×6×6×6×6= 6 \times 6 \times 6 \times 6 \times 6=
Get tutor helpright-arrow

Posted 3 months ago

Question
Write the expression in exponential form.\newline9×9×9×9×9×9×9= 9 \times 9 \times 9 \times 9 \times 9 \times 9 \times 9=
Get tutor helpright-arrow

Posted 3 months ago

Question
The value of Vishal's car is depreciating exponentially.\newlineThe relationship between V V , the value of his car, in dollars, and t t , the elapsed time, in years, since he purchased the car is modeled by the following equation.\newlineV=22,500⋅10−t12 V=22,500 \cdot 10^{-\frac{t}{12}} \newlineHow many years after purchase will Vishal's car be worth $10,000 \$ 10,000 ?\newlineGive an exact answer expressed as a base−10-10 logarithm.\newlineyears
Get tutor helpright-arrow

Posted 3 months ago

Question
A scientist measures the initial amount of Carbon−14-14 in a substance to be 2525 grams.\newlineThe relationship between A A , the amount of Carbon−14-14 remaining in that substance, in grams, and t t , the elapsed time, in years, since the initial measurement is modeled by the following equation.\newlineA=25e−0.00012t A=25 e^{-0.00012 t} \newlineIn how many years will the substance contain exactly 2020 grams (g) (\mathrm{g}) of Carbon−14-14?\newlineGive an exact answer expressed as a natural logarithm.\newlineyears
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following is equivalent to log⁡7(a)⋅log⁡b(7) \log _{7}(a) \cdot \log _{b}(7) ?\newlineChoose 11 answer:\newline(A) log⁡(7) \log (7) \newline(B) log⁡(7a) \log (7 a) \newline(C) log⁡a(b) \log _{a}(b) \newline(D) log⁡b(a) \log _{b}(a)
Get tutor helpright-arrow

Posted 3 months ago

Question
Which of the following is equivalent to log⁡(a)⋅log⁡a(5) \log (a) \cdot \log _{a}(5) ?\newlineChoose 11 answer:\newline(A) log⁡(a) \log (a) \newline(B) log⁡(5) \log (5) \newline(C) log⁡(5a) \log (5 a) \newline(D) log⁡a(5a) \log _{a}(5 a)
Get tutor helpright-arrow

Posted 3 months ago

View all (34)