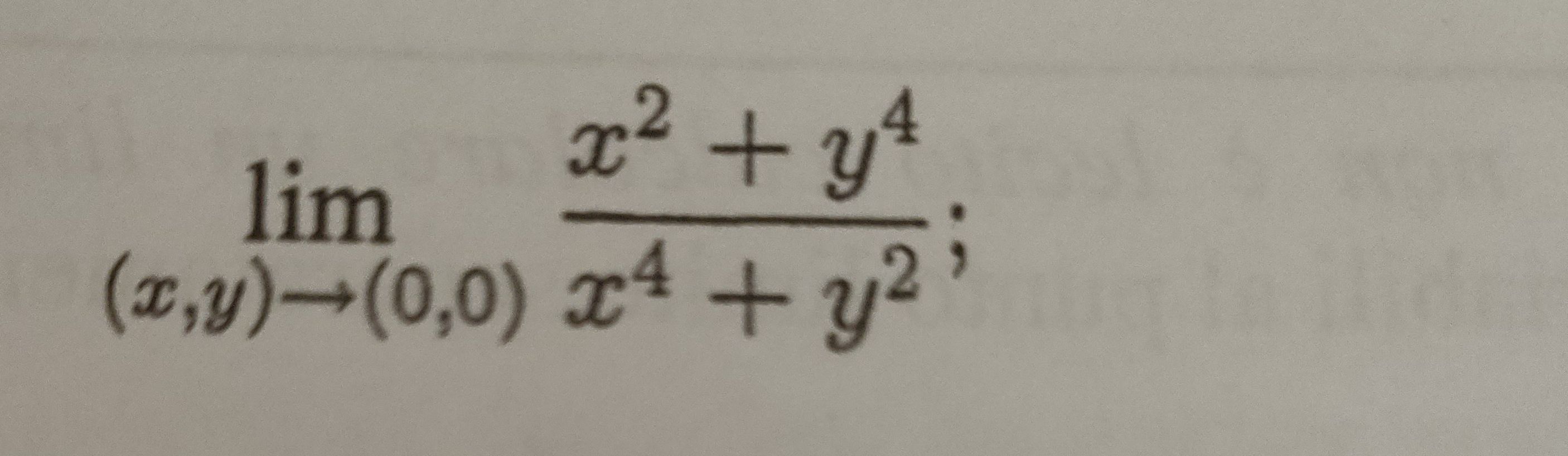AI tutor
Full solution
Q. Calculate the limit.
- Check Initial Value: First, let's plug in the values of and as to see if the function is defined at that point.We get an indeterminate form, so we need to do more work to find the limit.
- Approach Along y-axis: Let's try approaching along the y-axis .Simplify the expression.
- Approach Along x-axis: Now, let's approach along the x-axis .Simplify the expression.As approaches , approaches infinity.