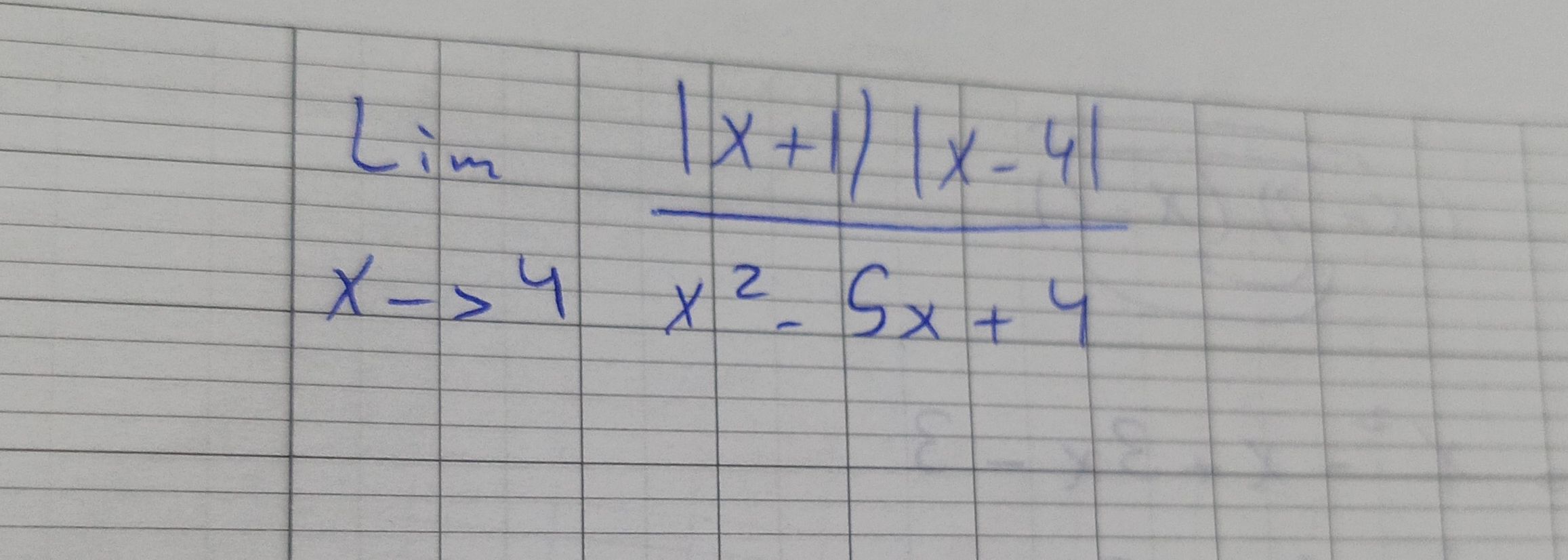AI tutor
Full solution
Q. Calculate the limit.
- Factor Denominator: First, let's factor the denominator.
- Rewrite Limit: Now, let's rewrite the limit with the factored denominator.
- Cancel Absolute Value: Notice that and will cancel each other out, but we need to be careful because of the absolute value.
- Split Limit into Cases: Since we're approaching from both sides, when x > 4 and when x < 4.
- Simplify Both Cases: So, we can split the limit into two cases, one for x > 4 and one for x < 4. For x > 4: For x < 4:
- Evaluate Absolute Value: Now, let's simplify both cases.For x > 4: For x < 4:
- Find Limits: As approaches , becomes which is .
- Find Limits: As approaches , becomes which is .So, we have:For x > 4: For x < 4:
- Find Limits: As approaches , becomes which is .So, we have:For x > 4: For x < 4: Now, let's find the limits.For x > 4: For x < 4: