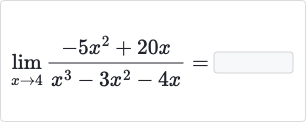lim_(x rarr4)(-5x^(2)+20 x)/(x^(3)-3x^(2)-4x)=

Question

Bytelearn · Accepted Answer

Identify Function: Identify the function to which we need to find the limit. We are given the function (-5x^2 + 20x) / (x^3 - 3x^2 - 4x) and we need to find its limit as x approaches 4.Substitute Value: Substitute the value of x into the function to see if it results in an indeterminate form. Let's substitute x = 4 into the function: (-5(4)^2 + 20(4)) / ((4)^3 - 3(4)^2 - 4(4)) = (-5(16) + 80) / (64 - 3(16) - 16) = (-80 + 80) / (64 - 48 - 16) = 0 / 0 We get an indeterminate form 0/0, which means we need to simplify the function further to find the limit.Factor Numerator and Denominator: Factor the numerator and the denominator of the function. We need to factor both the numerator and the denominator to see if there are common factors that can be canceled out. Numerator: -5x^2 + 20x can be factored as -5x(x - 4) Denominator: x^3 - 3x^2 - 4x can be factored as x(x^2 - 3x - 4) Further factor the quadratic x^2 - 3x - 4 as (x - 4)(x + 1) So the denominator becomes x(x - 4)(x + 1)Cancel Common Factors: Cancel out the common factors in the numerator and the denominator. We have a common factor of (x - 4) in both the numerator and the denominator. After canceling out the common factor, the function simplifies to: -5x / (x(x + 1)) = -5 / (x + 1)Substitute Simplified Function: Substitute the value of x into the simplified function to find the limit. Now that we have simplified the function, let's substitute x = 4 into the function: -5 / (4 + 1) = -5 / 5 = -1

$\lim _{x \rightarrow 4} \frac{-5 x^{2}+20 x}{x^{3}-3 x^{2}-4 x}=$

Full solution

More problems from Negative Exponents

Related topics

lim⁡x→4−5x2+20xx3−3x2−4x= \lim _{x \rightarrow 4} \frac{-5 x^{2}+20 x}{x^{3}-3 x^{2}-4 x}= limx→4​x3−3x2−4x−5x2+20x​=

$\lim _{x \rightarrow 4} \frac{-5 x^{2}+20 x}{x^{3}-3 x^{2}-4 x}=$