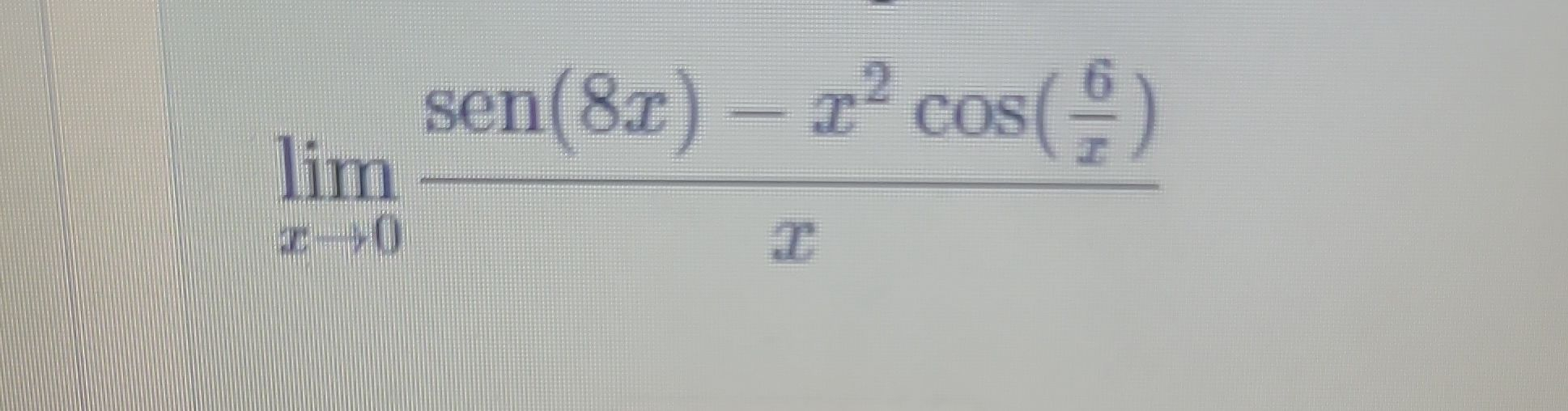Evaluate the limit. lim_(x rarr0)(sen(8x)-x^(2)cos((6)/(x)))/(x)

Question

Bytelearn · Accepted Answer

Identify Limit: Identify the limit that needs to be evaluated. We need to find the limit of the function (sin(8x) - x^2 cos(6/x)) / x as x approaches 0.Check Form: Check if the function is in an indeterminate form when x approaches 0. Plugging in x = 0, we get (sin(0) - 0^2 cos(6/0)) / 0, which is of the form 0/0, an indeterminate form.Apply L'Hôpital's Rule: Apply L'Hôpital's Rule since we have an indeterminate form of 0/0. L'Hôpital's Rule states that if the limit of f(x)/g(x) as x approaches a value c is of the form 0/0 or ∞/∞, then the limit is the same as the limit of f'(x)/g'(x) as x approaches c, provided that the latter limit exists.Differentiate Numerator and Denominator: Differentiate the numerator and the denominator separately. The derivative of the numerator sin(8x) with respect to x is 8cos(8x). The derivative of the numerator -x^2 cos(6/x) with respect to x is -2x cos(6/x) + (x^2)(6/x^2)sin(6/x) which simplifies to -2x cos(6/x) + 6sin(6/x). The derivative of the denominator x with respect to x is 1.Apply Derivatives to Rule: Apply the derivatives to L'Hôpital's Rule. Now we need to evaluate the limit of (8cos(8x) - 2x cos(6/x) + 6sin(6/x)) / 1 as x approaches 0.Evaluate Simplified Expression: Evaluate the limit of the simplified expression as x approaches 0. As x approaches 0, cos(8x) approaches cos(0) which is 1, and sin(6/x) approaches sin(∞) which oscillates and does not have a limit. However, since sin(6/x) is multiplied by x in the term 6sin(6/x), this term approaches 0. Therefore, the limit of the expression is 8(1) - 2(0)(cos(6/0)) + 6(0), which simplifies to 8.

Evaluate the limit. $\newline$ $\lim _{x \rightarrow 0} \frac{\operatorname{sin}(8 x)-x^{2} \cos \left(\frac{6}{x}\right)}{x}$

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

Evaluate the limit.\newlinelim⁡x→0sin⁡(8x)−x2cos⁡(6x)x \lim _{x \rightarrow 0} \frac{\operatorname{sin}(8 x)-x^{2} \cos \left(\frac{6}{x}\right)}{x} limx→0​xsin(8x)−x2cos(x6​)​

Evaluate the limit. $\newline$ $\lim _{x \rightarrow 0} \frac{\operatorname{sin}(8 x)-x^{2} \cos \left(\frac{6}{x}\right)}{x}$