Full solution
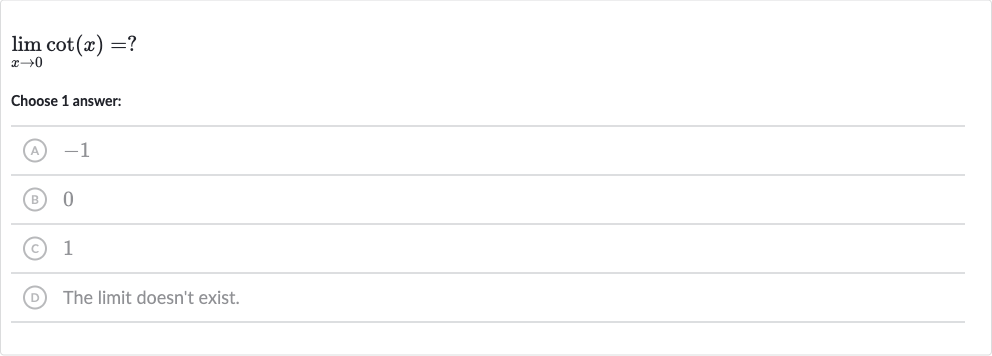
Q. Choose answer:(A) (B) (C) (D) The limit doesn't exist.
- Understanding cotangent function: To solve the limit of as approaches , we need to understand the behavior of the cotangent function near . The cotangent function, , is defined as the reciprocal of the tangent function, so .
- Behavior of cot() near : We know that approaches as approaches . Since is the reciprocal of , as gets smaller and smaller, will get larger and larger in magnitude. This means that the limit of as approaches from the right () will approach positive infinity, and from the left () will approach negative infinity.
- Limit of as approaches : Because the behavior of as approaches from the right is different from the behavior as approaches from the left, the limit does not exist. The function does not approach a single finite value from both sides.