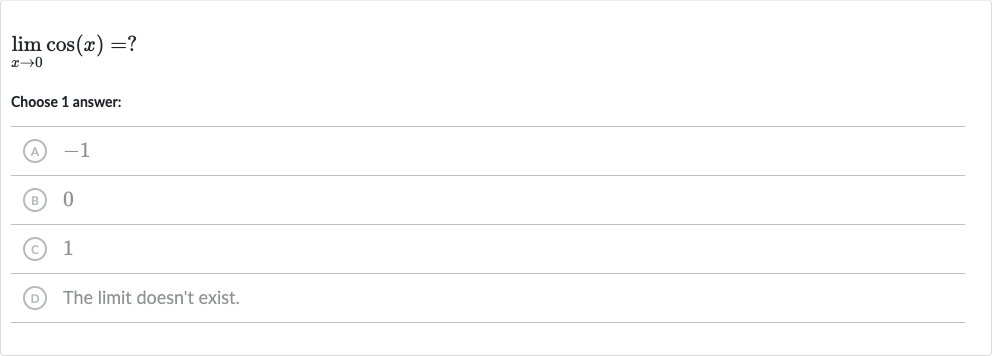
Full solution
Q. Choose answer:(A) (B) (C) (D) The limit doesn't exist.
- Evaluate the limit: To solve the limit problem, we need to evaluate the limit of the cosine function as approaches .
- Cosine of degrees: We know from trigonometry that the cosine of degrees (or radians) is equal to .
- Limit of as approaches : Therefore, the limit of as approaches is equal to .