Full solution
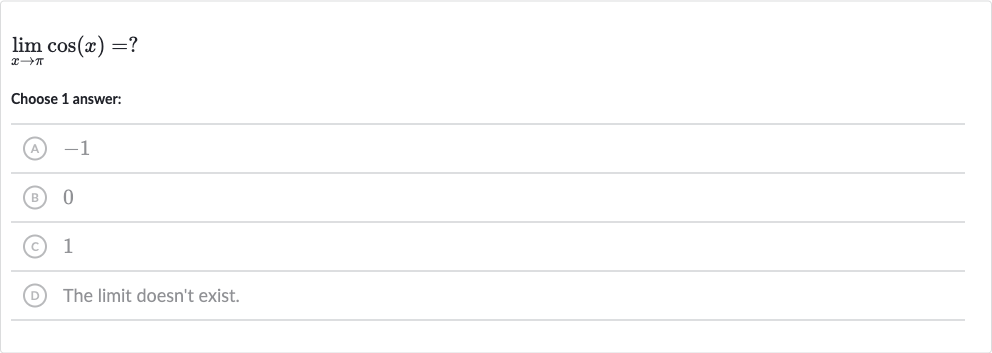
Q. Choose answer:(A) (B) (C) (D) The limit doesn't exist.
- Evaluate Cosine Function: To solve the limit problem, we need to evaluate the cosine function as the variable approaches the value of . The cosine function is continuous everywhere, so we can find the limit by direct substitution.
- Substitute with : Substitute with in the cosine function: .
- Use Trigonometric Identities: Using the unit circle or trigonometric identities, we know that equals .
- Find the Limit: Therefore, the limit of as approaches is .