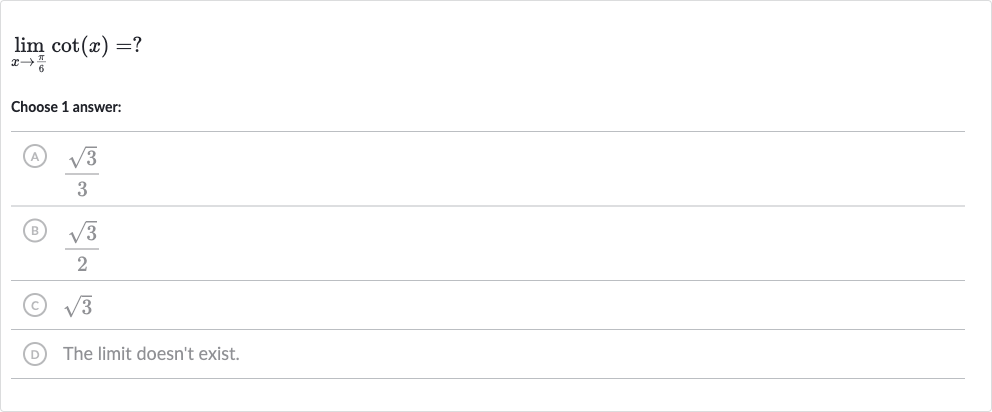
lim_(x rarr(pi)/(6))cot(x)=? Choose 1 answer: (A) (sqrt3)/(3) (B) (sqrt3)/(2) (C) sqrt3 (D) The limit doesn't exist.

Question

lim_(x rarr(pi)/(6))cot(x)=? Choose 1 answer: (A)  (sqrt3)/(3) (B)  (sqrt3)/(2) (C)  sqrt3 (D) The limit doesn't exist.

Bytelearn · Accepted Answer

Definition of cotangent: To find the limit of cot(x) as x approaches π/6, we need to understand the definition of cotangent. Cotangent is the reciprocal of the tangent function, so cot(x) = 1/tan(x).Finding tan(π/6): We know that tan(π/6) is equal to √3/3 because tan(x) is the ratio of the opposite side to the adjacent side in a right-angled triangle, and for an angle of π/6 (30 degrees), this ratio is √3/3.Reciprocal of tan(π/6): Therefore, cot(π/6) is the reciprocal of tan(π/6), which means cot(π/6) = 1/(√3/3). To find this value, we multiply the numerator and denominator by 3 to get rid of the fraction in the denominator.Rationalizing the denominator: After simplifying, we get cot(π/6) = 3/√3. To rationalize the denominator, we multiply the numerator and denominator by √3.Simplifying cot(π/6): This gives us cot(π/6) = (3√3)/(√3√3) which simplifies to cot(π/6) = (3√3)/3.Final result: After canceling out the 3 in the numerator and denominator, we are left with cot(π/6) = √3.

$\lim _{x \rightarrow \frac{\pi}{6}} \cot (x)=?$ $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{\sqrt{3}}{3}$ $\newline$ (B) $\frac{\sqrt{3}}{2}$ $\newline$ (C) $\sqrt{3}$ $\newline$ (D) The limit doesn't exist.

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

lim⁡x→π6cot⁡(x)=? \lim _{x \rightarrow \frac{\pi}{6}} \cot (x)=? x→6π​lim​cot(x)=?\newlineChoose 111 answer:\newline(A) 33 \frac{\sqrt{3}}{3} 33​​\newline(B) 32 \frac{\sqrt{3}}{2} 23​​\newline(C) 3 \sqrt{3} 3​\newline(D) The limit doesn't exist.

$\lim _{x \rightarrow \frac{\pi}{6}} \cot (x)=?$ $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{\sqrt{3}}{3}$ $\newline$ (B) $\frac{\sqrt{3}}{2}$ $\newline$ (C) $\sqrt{3}$ $\newline$ (D) The limit doesn't exist.