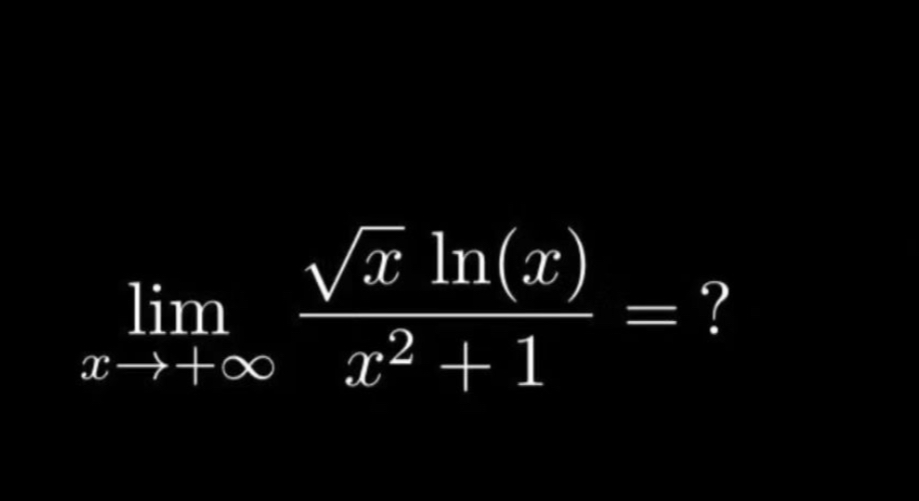Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

lim_(x rarr+oo)(sqrtxln(x))/(x^(2)+1)=?

$\lim _{x \rightarrow+\infty} \frac{\sqrt{x} \ln (x)}{x^{2}+1}=?$

View step-by-step help

View step-by-step help

Find derivatives using the chain rule I

Full solution

Q.

\lim _{x \rightarrow+\infty} \frac{\sqrt{x} \ln (x)}{x^{2}+1}=?

Recognize growth rates: First, recognize the growth rates of functions involved. The numerator $\sqrt{x} \cdot \ln(x)$ grows slower than the denominator $x^2$ .
Rewrite expression: Rewrite the expression for clarity: $(\sqrt{x} * \ln(x)) / (x^2 + 1) = (x^{1/2} * \ln(x)) / (x^2 + 1)$ .
Simplify by division: Simplify the expression by dividing each term in the numerator by $x^2$ : $(x^{1/2} / x^2) \cdot \ln(x) = (1 / x^{3/2}) \cdot \ln(x)$ .
Consider limits at infinity: As $x$ approaches infinity, $\frac{1}{x^{3/2}}$ approaches $0$ . Consider the behavior of $\ln(x)$ as $x$ approaches infinity; $\ln(x)$ increases, but at a slower rate compared to any power of $x$ .
Multiply the limits: Multiply the two limits: since $\frac{1}{x^{3/2}}$ approaches $0$ and $\ln(x)$ approaches infinity, the product $\left(\frac{1}{x^{3/2}}\right) * \ln(x)$ approaches $0$ .

More problems from Find derivatives using the chain rule I

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago