AI tutor
Full solution
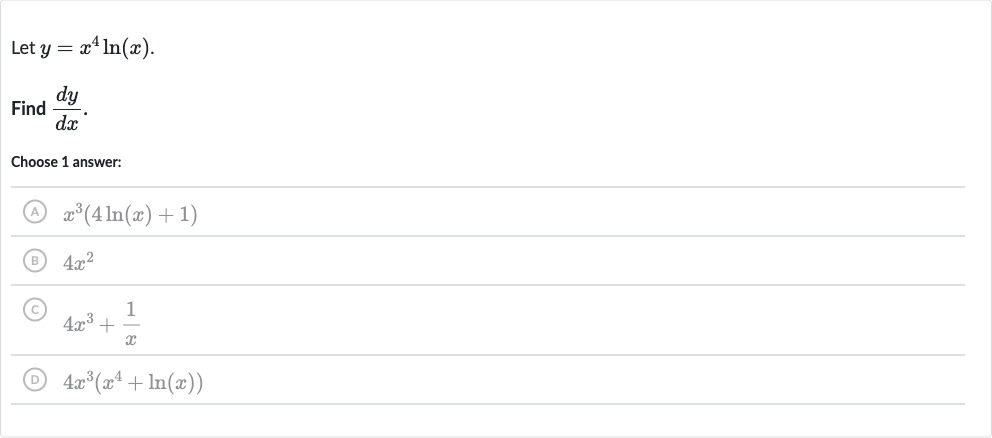
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Apply Product Rule: Using the product rule: , where and .
- Find : First, find the derivative of , which is .
- Find : Now, find the derivative of , which is .
- Apply Product Rule: Apply the product rule: .
- Simplify Expression: Simplify the expression: . Oops, there's a mistake here. We need to multiply by in the second term.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help