AI tutor
Full solution
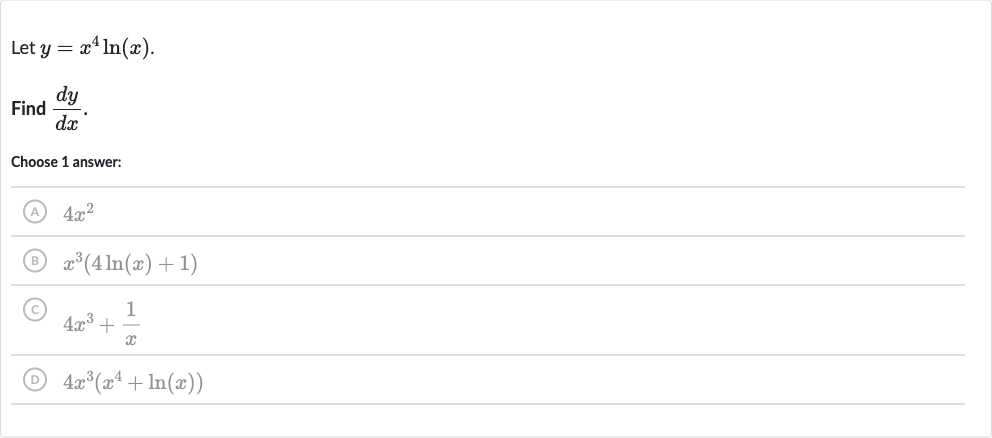
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Apply Product Rule: Using the product rule, which states that , where and . Differentiate with respect to to get .
- Differentiate : Now, differentiate with respect to to get .
- Differentiate : Plug , , , and into the product rule formula: .
- Apply Product Rule Formula: Simplify the expression:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help