Full solution
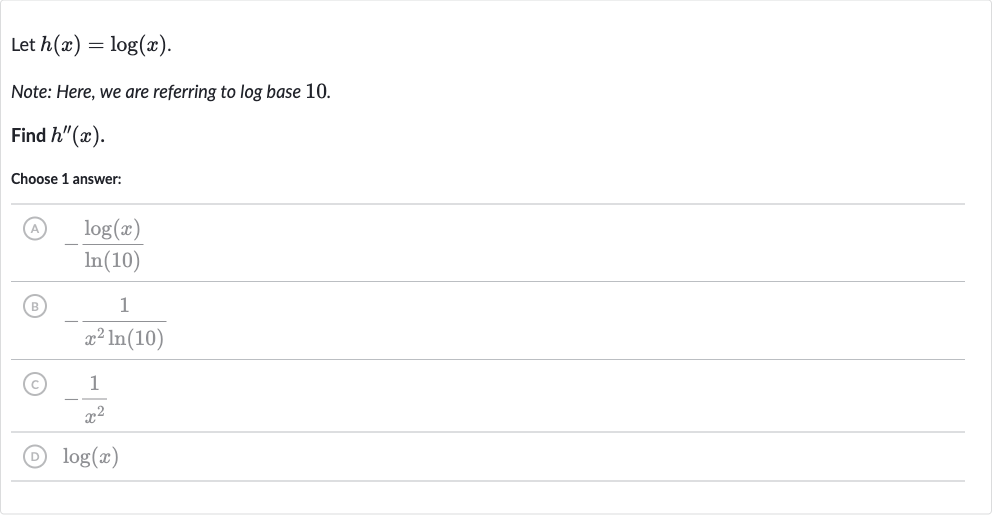
Q. Let .Note: Here, we are referring to log base .Find .Choose answer:(A) (B) (C) (D)
- Identify derivative of : Identify the first derivative of . The first derivative of the logarithm function with respect to is given by the formula:
- Differentiate : Differentiate to find the second derivative . To find , we take the derivative of with respect to : Using the quotient rule or recognizing this as the derivative of a reciprocal function, we get:
More problems from Properties of logarithms: mixed review
QuestionGet tutor help
QuestionGet tutor help