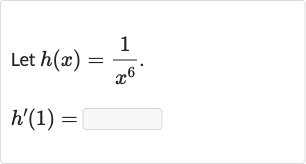AI tutor
Full solution
Q. Let .
- Differentiate function : Differentiate the function with respect to . To differentiate , we use the power rule for derivatives, which states that the derivative of with respect to is . In this case, we can rewrite as and then apply the power rule.
- Apply power rule: Evaluate the derivative at . We substitute into the derivative we found in Step . Since any number to the power of is just its reciprocal raised to the th power, and the reciprocal of is still , we have:
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help