AI tutor
Full solution
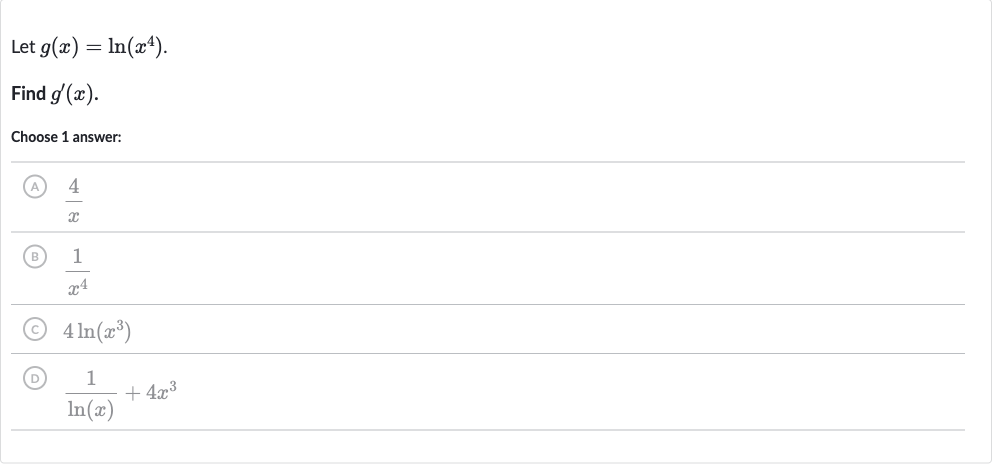
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Apply Chain Rule: Apply the chain rule to differentiate . The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. Here, the outer function is and the inner function is . The derivative of with respect to is , and the derivative of with respect to is . So, g'(x) = \left(\frac{\(1\)}{u}\right) \cdot \left(\frac{du}{dx}\right) = \left(\frac{\(1\)}{x^{\(4\)}}\right) \cdot \left(\(4x^{}\right)\.
- Simplify Expression: Simplify the expression for . We have . When we multiply the fractions, we can cancel out from the numerator and denominator. This gives us .
- Match Answer Choices: Match the simplified expression to the given answer choices.The simplified expression for the derivative is , which corresponds to answer choice (A) .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help