AI tutor
Full solution
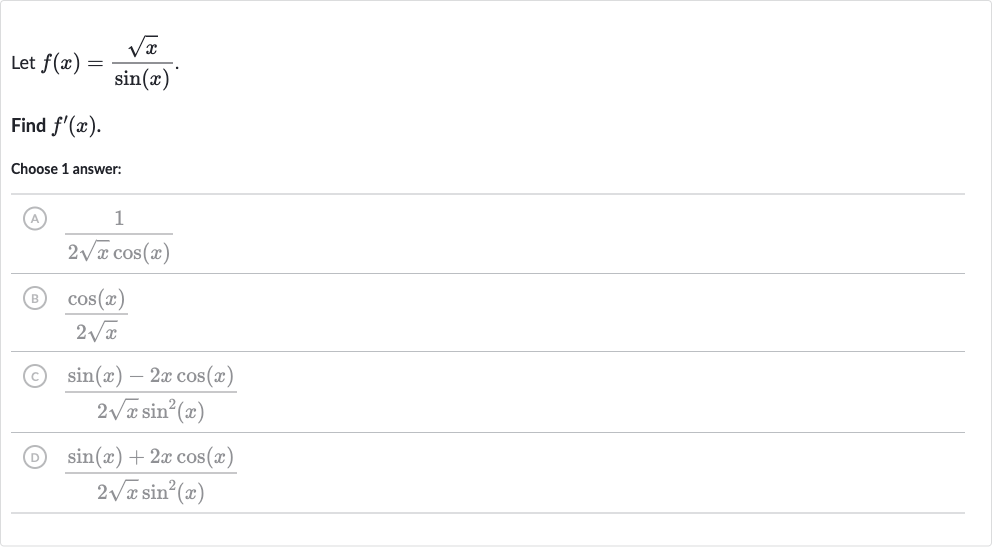
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Identify Function: Identify the function to differentiate. is a quotient of two functions, where the numerator is and the denominator is .
- Apply Quotient Rule: Apply the quotient rule for differentiation.The quotient rule states that , where is the numerator and is the denominator.Let and . We need to find and .
- Differentiate and : Differentiate and .
, so .
, so . - Apply Derivatives: Apply the derivatives to the quotient rule. = = =
- Choose Correct Answer: Choose the correct answer.The correct answer is (C) .
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help