AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
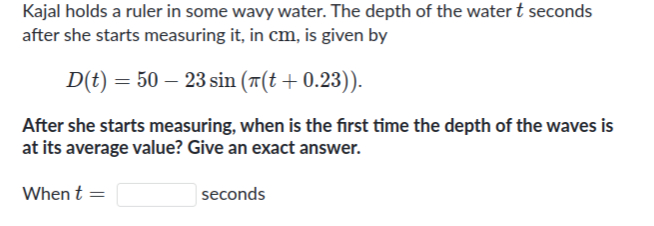
Kajal holds a ruler in some wavy water. The depth of the water seconds after she starts measuring it, in , is given byAfter she starts measuring, when is the first time the depth of the waves is at its average value? Give an exact answer.When seconds
Full solution
Q. Kajal holds a ruler in some wavy water. The depth of the water seconds after she starts measuring it, in , is given byAfter she starts measuring, when is the first time the depth of the waves is at its average value? Give an exact answer.When seconds
- Find Average Depth: To find the average value of the wave depth, we need to determine the constant term in the equation . The average depth is the constant term since the average value of the sine function over its period is zero.Calculation: Average depth = cm.
- Set Depth to Average: Next, we need to find when the depth equals the average depth. Set to : Calculation:
- Solve for Sine Function: Solve for . The sine function equals zero at integer multiples of .Calculation: , where is an integer.
- Calculate t Value: Solve for : .Calculation: .
- Determine Smallest Positive : The smallest positive value for occurs when (since gives a negative time, which doesn't make sense in this context).Calculation: seconds.
More problems from Evaluate two-variable equations: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
