AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
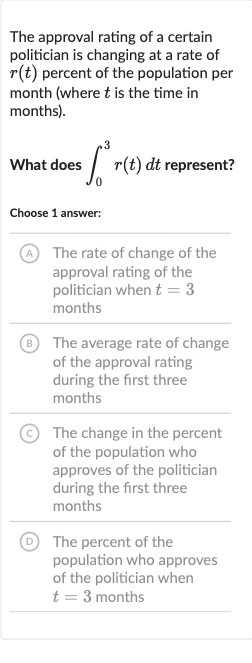
The approval rating of a certain politician is changing at a rate of percent of the population per month (where is the time in months).What does represent?Choose answer:(A) The rate of change of the approval rating of the politician when months(B) The average rate of change of the approval rating during the first three months(C) The change in the percent of the population who approves of the politician during the first three months(D) The percent of the population who approves of the politician when months
Full solution
Q. The approval rating of a certain politician is changing at a rate of percent of the population per month (where is the time in months).What does represent?Choose answer:(A) The rate of change of the approval rating of the politician when months(B) The average rate of change of the approval rating during the first three months(C) The change in the percent of the population who approves of the politician during the first three months(D) The percent of the population who approves of the politician when months
- Understand the integral: Understand the integral in the context of the problem.The integral of a rate of change function over an interval gives the net change over that interval. In this case, represents the rate of change of the politician's approval rating over time, so the integral from to of represents the total change in approval rating over the first three months.
- Match with answer choices: Match the integral's meaning to the given answer choices.The integral does not represent the rate of change at a specific time (which would be given by itself, not the integral), so option (A) is incorrect. It also does not represent an average rate of change, which would be the integral divided by the time interval, so option (B) is incorrect. It does not give the percent of the population who approves at a specific time, so option (D) is incorrect. The integral represents the total change in approval rating over the time interval, which matches option (C).
- Confirm final answer: Confirm the final answer.The integral from to of represents the change in the percent of the population who approves of the politician during the first three months, which is option (C).
More problems from Evaluate two-variable equations: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
