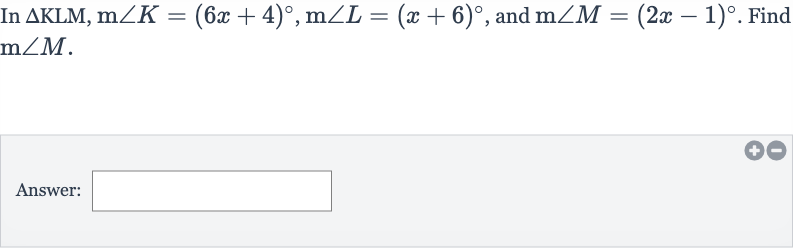
In /_\KLM,m/_K=(6x+4)^(@),m/_L=(x+6)^(@), and m/_M=(2x-1)^(@). Find m/_M. Answer:

Question

In  /_\KLM,m/_K=(6x+4)^(@),m/_L=(x+6)^(@), and  m/_M=(2x-1)^(@). Find  m/_M. Answer:

Bytelearn · Accepted Answer

Triangle Angle Sum: In triangle KLM, the sum of the angles must equal 180 degrees. This is a fundamental property of triangles. Calculation: m/_K + m/_L + m/_M = 180 degrees Substitute the given expressions for m/_K and m/_L: (6x+4) + (x+6) + m/_M = 180Simplify Equation: Combine like terms to simplify the equation. Calculation: (6x + x) + (4 + 6) + m/_M = 180 7x + 10 + m/_M = 180Isolate Terms: Subtract 10 from both sides to isolate terms with x on one side and constants on the other. Calculation: 7x + m/_M = 180 - 10 7x + m/_M = 170Substitute Expression: We know that m/_M = (2x-1) degrees, so we can substitute this expression into our equation. Calculation: 7x + (2x - 1) = 170Combine Like Terms: Combine like terms to solve for x. Calculation: 7x + 2x - 1 = 170 9x - 1 = 170Solve for x: Add 1 to both sides to isolate the term with x. Calculation: 9x = 170 + 1 9x = 171Find m/M: Divide both sides by 9 to solve for x. Calculation: x = 171 / 9 x = 19Final Calculation: Now that we have the value of x, we can find m/_M by substituting x back into the expression for m/_M. Calculation: m/_M = (2x - 1) m/_M = (2*19 - 1) m/_M = (38 - 1) m/_M = 37 degrees

In $\triangle \mathrm{KLM}, \mathrm{m} \angle K=(6 x+4)^{\circ}, \mathrm{m} \angle L=(x+6)^{\circ}$ , and $\mathrm{m} \angle M=(2 x-1)^{\circ}$ . Find $\mathrm{m} \angle M$ . $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics