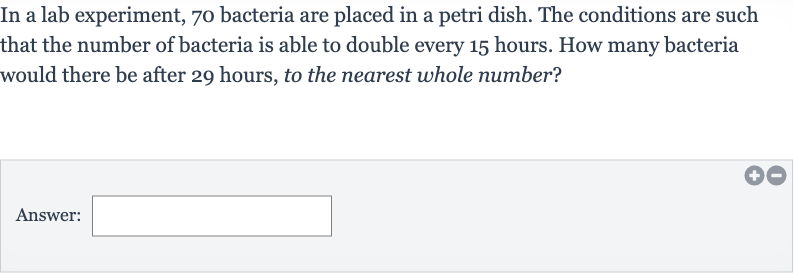
In a lab experiment, $70$ bacteria are placed in a petri dish. The conditions are such that the number of bacteria is able to double every $15$ hours. How many bacteria would there be after $29$ hours, to the nearest whole number? $\newline$ Answer:

View step-by-step help

Home

Math Problems

Grade 7

Convert between customary and metric systems

Full solution

Q. In a lab experiment,

70

bacteria are placed in a petri dish. The conditions are such that the number of bacteria is able to double every

15

hours. How many bacteria would there be after

29

hours, to the nearest whole number?

\newline

Answer:

Determine Doubling Periods: First, we need to determine how many times the bacteria population can double in $29$ hours. Since the bacteria double every $15$ hours, we divide the total time by the doubling period. $\newline$ $29$ hours $\div$ $15$ hours per doubling period = $1.9333$ doubling periods.
Calculate Full Periods: Since the bacteria can only double an integer number of times, we need to consider how many full doubling periods occur within $29$ hours. We can't have a fraction of a doubling period, so we take the floor of the previous result. $\newline$ Full doubling periods = $1$ (since $1.9333$ indicates that only one full doubling period has occurred within $29$ hours).
Calculate After $1$ Period: Now we calculate the number of bacteria after one full doubling period. We start with $70$ bacteria and double it once. $\newline$ Number of bacteria after $1$ doubling period = $70 \times 2^1 = 70 \times 2 = 140$ bacteria.
Estimate Growth: We have $14$ hours remaining after the first doubling period ( $29$ hours - $15$ hours = $14$ hours). We need to estimate the growth during this period. Since the bacteria double every $15$ hours, we can use the fraction of the doubling period that has passed ( $\frac{14}{15}$ ) to estimate the growth. $\newline$ Fraction of doubling period passed = $\frac{14}{15}$ .
Calculate Growth Factor: We calculate the growth factor for the remaining $14$ hours using the fraction of the doubling period. $\newline$ Growth factor for $14$ hours = $2^{(14/15)}$ .
Apply Growth Factor: Now we apply the growth factor to the number of bacteria after the first doubling period to estimate the total number of bacteria after $29$ hours. $\newline$ Estimated number of bacteria after $29$ hours $= 140 \times 2^{\frac{14}{15}}$ .
Calculate Estimated Bacteria: We perform the calculation for the growth factor and then multiply by the number of bacteria after the first doubling period. $\newline$ $2^{\frac{14}{15}} \approx 1.897$ (rounded to three decimal places for simplicity). $\newline$ Estimated number of bacteria after $29$ hours $\approx 140 \times 1.897$ .
Round to Nearest Whole: Finally, we calculate the estimated number of bacteria to the nearest whole number. $\newline$ Estimated number of bacteria after $29$ hours $\approx 140 \times 1.897 \approx 265.58$ . $\newline$ Since we need to report the number of bacteria to the nearest whole number, we round $265.58$ to $266$ .