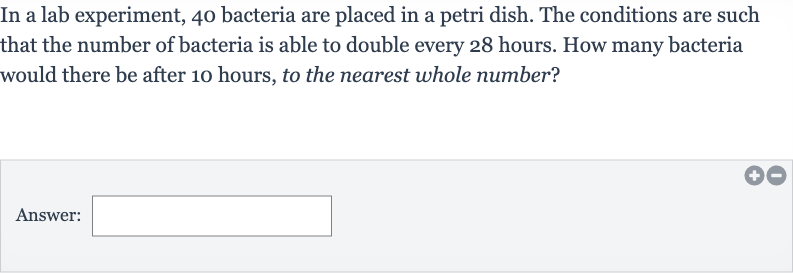
In a lab experiment, $40$ bacteria are placed in a petri dish. The conditions are such that the number of bacteria is able to double every $28$ hours. How many bacteria would there be after $10$ hours, to the nearest whole number? $\newline$ Answer:

View step-by-step help

Home

Math Problems

Grade 7

Convert between customary and metric systems

Full solution

Q. In a lab experiment,

40

bacteria are placed in a petri dish. The conditions are such that the number of bacteria is able to double every

28

hours. How many bacteria would there be after

10

hours, to the nearest whole number?

\newline

Answer:

Understand and Identify: Understand the problem and determine what is given and what needs to be found. $\newline$ We know: $\newline$ Initial number of bacteria: $40$ $\newline$ Doubling time: $28$ hours $\newline$ Time elapsed: $10$ hours $\newline$ We need to find the number of bacteria after $10$ hours.
Calculate Doubling Periods: Calculate the number of times the bacteria population will double in $10$ hours. $\newline$ Since the bacteria double every $28$ hours, we need to find out how many $28$ -hour periods fit into $10$ hours. However, since $10$ hours is less than $28$ hours, the bacteria will not have doubled even once in that time frame.
Determine Growth Rate: Determine the growth rate per hour. $\newline$ To find the growth rate per hour, we assume exponential growth and use the formula for exponential growth: $N = N_0 \cdot e^{kt}$ , where $N$ is the final amount, $N_0$ is the initial amount, $k$ is the growth rate, and $t$ is the time in hours. Since we don't have a full doubling period, we need to solve for $k$ using the doubling time. $\newline$ Doubling formula: $N = N_0 \cdot 2^{\frac{t}{T}}$ , where $T$ is the doubling time. $\newline$ $2 = e^{k\cdot 28}$ $\newline$ $k = \frac{\ln(2)}{28}$
Calculate Growth Rate: Calculate the growth rate $k$ . $\newline$ $k = \frac{\ln(2)}{28}$ $\newline$ $k \approx 0.0248$ (rounded to four decimal places)
Use Growth Rate: Use the growth rate to calculate the number of bacteria after $10$ hours. $\newline$ $N = 40 \times e^{(0.0248\times10)}$ $\newline$ $N \approx 40 \times e^{(0.248)}$
Evaluate Expression: Evaluate the expression to find the final number of bacteria. $\newline$ $N \approx 40 \times e^{0.248}$ $\newline$ $N \approx 40 \times 1.282$ (using a calculator for $e^{0.248}$ ) $\newline$ $N \approx 51.28$
Round Final Result: Round the number of bacteria to the nearest whole number. $\newline$ The number of bacteria after $10$ hours, rounded to the nearest whole number, is approximately $51$ .