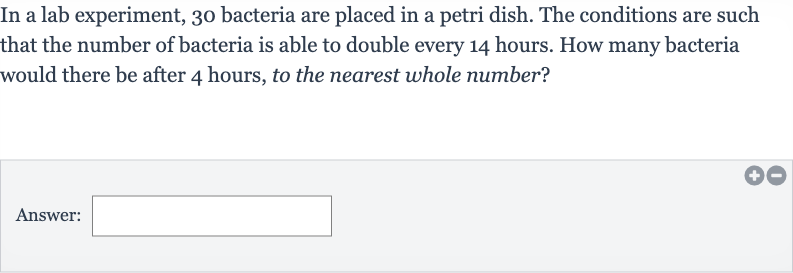
In a lab experiment, $30$ bacteria are placed in a petri dish. The conditions are such that the number of bacteria is able to double every $14$ hours. How many bacteria would there be after $4$ hours, to the nearest whole number? $\newline$ Answer:

View step-by-step help

Home

Math Problems

Grade 7

Convert between customary and metric systems

Full solution

Q. In a lab experiment,

30

bacteria are placed in a petri dish. The conditions are such that the number of bacteria is able to double every

14

hours. How many bacteria would there be after

4

hours, to the nearest whole number?

\newline

Answer:

Understand the problem: Understand the problem and determine what is being asked. $\newline$ We need to calculate the number of bacteria after $4$ hours, knowing that the initial count is $30$ and they double every $14$ hours. Since $4$ hours is not a full doubling period, we need to find out how much growth occurs in $4$ hours as a fraction of the $14$ -hour doubling period.
Calculate fraction of period: Calculate the fraction of the doubling period that has passed after $4$ hours. $\newline$ $4$ hours is $\frac{4}{14}$ of the $14$ -hour period. $\newline$ Fraction of the doubling period = $\frac{4}{14}$
Convert fraction to growth factor: Convert the fraction of the doubling period into a growth factor. $\newline$ Since the bacteria double every full period, we need to find the growth factor for the fraction of the period. This can be done using the formula for exponential growth: $N = N_0 \times 2^{\frac{t}{T}}$ , where $N$ is the final amount, $N_0$ is the initial amount, $t$ is the time elapsed, and $T$ is the doubling time. $\newline$ Growth factor for $4$ hours = $2^{\frac{4}{14}}$
Calculate growth factor: Calculate the growth factor using the fraction obtained in Step $2$ . $\newline$ Growth factor for $4$ hours = $2^{\frac{4}{14}} \approx 2^{0.2857}$ $\newline$ Using a calculator, we find that $2^{0.2857} \approx 1.3348$
Apply growth factor: Apply the growth factor to the initial number of bacteria to find the number after $4$ hours. $\newline$ Number of bacteria after $4$ hours $=$ Initial number of bacteria $*$ Growth factor $\newline$ Number of bacteria after $4$ hours $\approx 30 \times 1.3348$
Perform multiplication: Perform the multiplication to find the number of bacteria after $4$ hours. $\newline$ Number of bacteria after $4$ hours $\approx 30 \times 1.3348 \approx 40.044$
Round the result: Round the result to the nearest whole number, as the question asks for an approximation. $\newline$ Number of bacteria after $4$ hours, rounded = $40$ (to the nearest whole number)