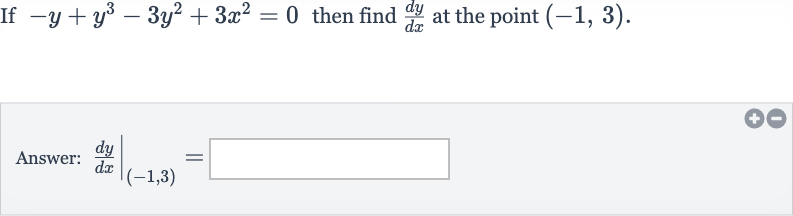
If -y+y^(3)-3y^(2)+3x^(2)=0 then find (dy)/(dx) at the point (-1,3). Answer: (dy)/(dx)|_((-1,3))=

Question

If  -y+y^(3)-3y^(2)+3x^(2)=0 then find  (dy)/(dx) at the point  (-1,3). Answer:  (dy)/(dx)|_((-1,3))=

Bytelearn · Accepted Answer

Implicit Differentiation: To find the derivative (dy)/(dx), we need to implicitly differentiate the given equation with respect to x. The equation is -y + y^3 - 3y^2 + 3x^2 = 0.Chain Rule Application: Differentiate each term with respect to x. For terms with y, we use the chain rule, treating y as a function of x (y(x)). The derivative of -y with respect to x is -dy/dx. The derivative of y^3 with respect to x is 3y^2 * dy/dx by the chain rule. The derivative of -3y^2 with respect to x is -6y * dy/dx by the chain rule. The derivative of 3x^2 with respect to x is 6x.Grouping Terms: Writing the derivatives out, we get: -dy/dx + 3y^2 * dy/dx - 6y * dy/dx + 6x = 0.Factor Out dy/dx: Now we group the terms with dy/dx on one side and the term with x on the other side: -dy/dx + 3y^2 * dy/dx - 6y * dy/dx = -6x.Solve for dy/dx: Factor out dy/dx from the left side of the equation: dy/dx * (-1 + 3y^2 - 6y) = -6x.Substitute Values: Solve for dy/dx by dividing both sides by (-1 + 3y^2 - 6y): dy/dx = -6x / (-1 + 3y^2 - 6y).Calculate Denominator: Now we need to evaluate dy/dx at the point (-1,3). Substitute x = -1 and y = 3 into the equation: dy/dx|_((-1,3)) = -6(-1) / (-1 + 3(3)^2 - 6(3)).Calculate Numerator: Calculate the denominator: -1 + 3(3)^2 - 6(3) = -1 + 3(9) - 18 = -1 + 27 - 18 = 8.Divide to Find dy/dx: Calculate the numerator: -6(-1) = 6.Simplify Fraction: Now, divide the numerator by the denominator to find dy/dx at the point (-1,3): dy/dx|_((-1,3)) = 6 / 8.Simplify the fraction: dy/dx|_((-1,3)) = 3 / 4.

If $-y+y^{3}-3 y^{2}+3 x^{2}=0$ then find $\frac{d y}{d x}$ at the point $(-1,3)$ . $\newline$ Answer: $\left.\frac{d y}{d x}\right|_{(-1,3)}=$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

If −y+y3−3y2+3x2=0 -y+y^{3}-3 y^{2}+3 x^{2}=0 −y+y3−3y2+3x2=0 then find dydx \frac{d y}{d x} dxdy​ at the point (−1,3) (-1,3) (−1,3).\newlineAnswer: dydx∣(−1,3)= \left.\frac{d y}{d x}\right|_{(-1,3)}= dxdy​∣∣​(−1,3)​=

If $-y+y^{3}-3 y^{2}+3 x^{2}=0$ then find $\frac{d y}{d x}$ at the point $(-1,3)$ . $\newline$ Answer: $\left.\frac{d y}{d x}\right|_{(-1,3)}=$