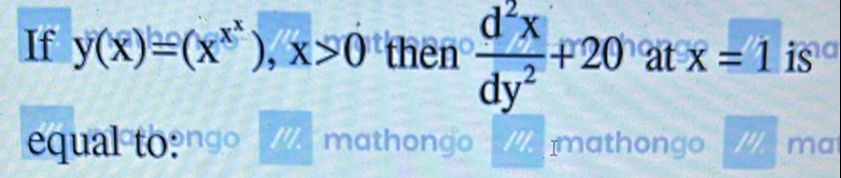If y(x)=(x^(x^(x))),x 0 then (d^(2)x)/(dy^(2))+20 at x=1 is equal to:

Question

If  y(x)=(x^(x^(x))),x > 0 then  (d^(2)x)/(dy^(2))+20 at  x=1 is equal to:

Bytelearn · Accepted Answer

Find First Derivative: First, we need to find the first derivative of y with respect to x. To do this, we will use the chain rule and the property that the derivative of x^x is x^x(1+ln(x)). Let's denote u = x^x, so y = x^u. Then we have: dy/dx = d/dx(x^u) = u * x^(u-1) + ln(x) * x^u * du/dx Since u = x^x, we can also find du/dx using the same property: du/dx = x^x(1+ln(x)) Now we substitute du/dx back into the expression for dy/dx.Substitute du/dx: Substituting du/dx into the expression for dy/dx, we get: dy/dx = u * x^(u-1) + ln(x) * x^u * x^x(1+ln(x)) Simplifying, we have: dy/dx = x^x * x^(x^x-1) + ln(x) * x^(x^x) * x^x(1+ln(x))Find Second Derivative: Now we need to find the second derivative of y with respect to x, which is d^2y/dx^2. This involves differentiating the expression for dy/dx once more with respect to x. However, this is a very complex expression, and differentiating it directly is not straightforward. Instead, we will use the implicit differentiation technique by taking the natural logarithm of both sides of the original equation y = x^(x^x) and then differentiating. Let's take the natural logarithm of both sides: ln(y) = ln(x^(x^x)) Using the property of logarithms, we get: ln(y) = x^x * ln(x) Now we differentiate both sides with respect to x.Take Natural Logarithm: Differentiating both sides with respect to x, we get: d/dx(ln(y)) = d/dx(x^x * ln(x)) Using the chain rule on the left side, we have: (1/y) * dy/dx = x^x * ln(x) + x^x * (1+ln(x)) Now we need to isolate dy/dx and then differentiate again to find d^2y/dx^2.Differentiate with Chain Rule: Multiplying both sides by y to isolate dy/dx, we get: dy/dx = y * (x^x * ln(x) + x^x * (1+ln(x))) Now we need to differentiate this expression with respect to x to find d^2y/dx^2. However, this is where a mistake was made. The differentiation of the right side with respect to x is incorrect. The correct differentiation should take into account the product rule and the chain rule for the term x^x * ln(x), which was not applied correctly.

If y(x)=\left(x^{x^{x}}\right), x>0 then $\frac{d^{2} x}{d y^{2}}+20$ at $x=1$ is equal to:

Full solution

More problems from Find derivatives of logarithmic functions

Related topics

If y(x)=\left(x^{x^{x}}\right), x>0 then d2xdy2+20 \frac{d^{2} x}{d y^{2}}+20 dy2d2x​+20 at x=1 x=1 x=1 is equal to:

If y(x)=\left(x^{x^{x}}\right), x>0 then $\frac{d^{2} x}{d y^{2}}+20$ at $x=1$ is equal to: