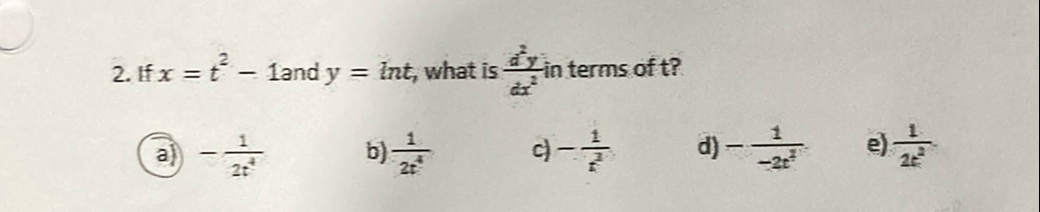If x=t^(2)-1 and y=ln t, what is (d^(2)y)/(dx^(2)) in terms of t ? (a) -(1)/(2t^(4)) b) (1)/(2t^(4)) c) -(1)/(x^(3)) d) -(1)/(-2t^(2)) e) (1)/(2t^(2))

Question

If  x=t^(2)-1 and  y=ln t, what is  (d^(2)y)/(dx^(2)) in terms of  t ? (a)  -(1)/(2t^(4)) b)  (1)/(2t^(4)) c)  -(1)/(x^(3)) d)  -(1)/(-2t^(2)) e)  (1)/(2t^(2))

Bytelearn · Accepted Answer

Find Derivative of y: First, we need to find the first derivative of y with respect to t, which is (dy)/(dt). Since y = ln t, we use the derivative of the natural logarithm function. (dy)/(dt) = 1/tFind Derivative of x: Next, we need to find the first derivative of x with respect to t, which is (dx)/(dt). Since x = t^2 - 1, we use the power rule for differentiation. (dx)/(dt) = 2tFind Derivative of y with x: Now, we will find the first derivative of y with respect to x, which is (dy)/(dx), using the chain rule. (dy)/(dx) = (dy)/(dt) * (dt)/(dx) We already have (dy)/(dt) = 1/t and (dx)/(dt) = 2t, so we need to find (dt)/(dx), which is the reciprocal of (dx)/(dt). (dt)/(dx) = 1 / (dx)/(dt) = 1 / (2t)Substitute Values for dy/dx: Substitute the values we have into the chain rule to find (dy)/(dx). (dy)/(dx) = (1/t) * (1 / (2t)) = 1 / (2t^2)Find Second Derivative of y with x: Now we need to find the second derivative of y with respect to x, which is (d^2y)/(dx^2). To do this, we differentiate (dy)/(dx) with respect to x. (d^2y)/(dx^2) = d/dx (1 / (2t^2))Differentiate 1/(2t^2) with t: To differentiate (1 / (2t^2)) with respect to x, we need to apply the chain rule again, since t is a function of x. (d^2y)/(dx^2) = d/dt (1 / (2t^2)) * (dt)/(dx)Substitute (dt)/(dx): First, differentiate 1 / (2t^2) with respect to t. d/dt (1 / (2t^2)) = d/dt (t^(-2) / 2) = -2 * t^(-3) / 2 = -1 / t^3Now, substitute (dt)/(dx) from the previous steps. (d^2y)/(dx^2) = (-1 / t^3) * (1 / (2t)) (d^2y)/(dx^2) = -1 / (2t^4)

If $x=t^{2}-1$ and $y=\ln t$ , what is $\frac{d^{2} y}{d x^{2}}$ in terms of $t$ ? $\newline$ (a) $-\frac{1}{2 t^{4}}$ $\newline$ b) $\frac{1}{2 t^{4}}$ $\newline$ c) $-\frac{1}{x^{3}}$ $\newline$ d) $-\frac{1}{-2 t^{2}}$ $\newline$ e) $\frac{1}{2 t^{2}}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics