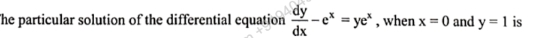Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

he particular solution of the differential equation
(dy)/(dx)-e^(x)=ye^(x), when
x=0 and
y=1 is

The particular solution of the differential equation $\frac{dy}{dx}-e^{x}=ye^{x}$ , when $x=0$ and $y=1$ is

View step-by-step help

View step-by-step help

Find derivatives using the quotient rule I

Full solution

Q. The particular solution of the differential equation

\frac{dy}{dx}-e^{x}=ye^{x}

, when

x=0

and

y=1

is

Rewrite Differential Equation: First, we need to rewrite the differential equation in a form that allows us to use the method of integrating factors. The equation is already in the form of a first-order linear differential equation, $\frac{dy}{dx} + P(x)y = Q(x)$ , where $P(x) = -e^x$ and $Q(x) = e^x$ .
Calculate Integrating Factor: Next, we calculate the integrating factor, $\mu(x)$ , which is $e^{(\int P(x)\,dx)}$ . In this case, $\mu(x) = e^{(\int -e^x\,dx)}$ . The integral of $-e^x$ with respect to $x$ is $-e^x$ , so $\mu(x) = e^{(-e^x)}$ .
Multiply by Integrating Factor: Now, we multiply the entire differential equation by the integrating factor, $\mu(x)$ , to get $\mu(x) \cdot \frac{dy}{dx} + \mu(x) \cdot P(x) \cdot y = \mu(x) \cdot Q(x)$ . Substituting the values of $\mu(x)$ , $P(x)$ , and $Q(x)$ , we get $e^{(-e^x)} \cdot \frac{dy}{dx} - e^{(-e^x)} \cdot e^x \cdot y = e^{(-e^x)} \cdot e^x$ .
Recognize Derivative Form: We notice that the left side of the equation is now the derivative of $(y \cdot \mu(x))$ with respect to $x$ . Therefore, we can write $\frac{d}{dx}(y \cdot e^{(-e^x)}) = e^{(-e^x)} \cdot e^x$ .
Integrate Both Sides: To solve for $y$ , we integrate both sides of the equation with respect to $x$ . The integral of the left side is $y \cdot e^{-e^x}$ , and the integral of the right side is $\int e^{-e^x} \cdot e^x \, dx$ .
Re-evaluate Integrating Factor: The integral on the right side is not a standard integral and cannot be expressed in terms of elementary functions. It seems there has been a mistake in the calculation of the integrating factor or in the setup of the equation. We need to re-evaluate the integrating factor and the setup of the equation.

More problems from Find derivatives using the quotient rule I

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago