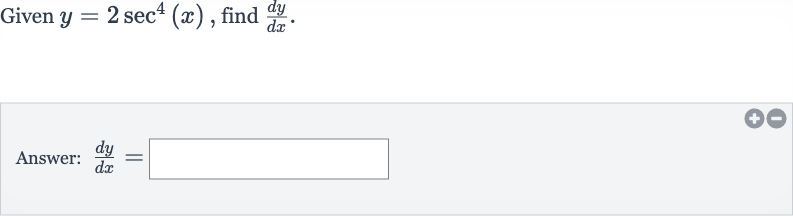
Given y=2sec^(4)(x), find (dy)/(dx). Answer: (dy)/(dx)=

Question

Given  y=2sec^(4)(x), find  (dy)/(dx). Answer:  (dy)/(dx)=

Bytelearn · Accepted Answer

Identify Functions: To find the derivative of y with respect to x, we need to apply the chain rule to the function y = 2sec^4(x). The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.Derivative of Outer Function: First, let's identify the outer function and the inner function. The outer function is u^4 where u = sec(x), and the inner function is sec(x). We will need to take the derivative of the outer function with respect to u and then multiply it by the derivative of the inner function with respect to x.Derivative of Inner Function: The derivative of the outer function u^4 with respect to u is 4u^3. So, if u = sec(x), then the derivative of u^4 with respect to x is 4sec^3(x).Combine Derivatives: Now we need to find the derivative of the inner function sec(x) with respect to x. The derivative of sec(x) is sec(x)tan(x). So, the derivative of sec^4(x) with respect to x is 4sec^3(x) times sec(x)tan(x).Final Derivative: Multiplying the derivatives together, we get the derivative of y with respect to x: (dy/dx) = 2 * 4sec^3(x) * sec(x)tan(x).Simplify the expression by combining like terms and constants: (dy/dx) = 8sec^4(x)tan(x).

Given $y=2 \sec ^{4}(x)$ , find $\frac{d y}{d x}$ . $\newline$ Answer: $\frac{d y}{d x}=$

Full solution

More problems from Simplify variable expressions using properties

Related topics

Given y=2sec⁡4(x) y=2 \sec ^{4}(x) y=2sec4(x), find dydx \frac{d y}{d x} dxdy​.\newlineAnswer: dydx= \frac{d y}{d x}= dxdy​=

Given $y=2 \sec ^{4}(x)$ , find $\frac{d y}{d x}$ . $\newline$ Answer: $\frac{d y}{d x}=$