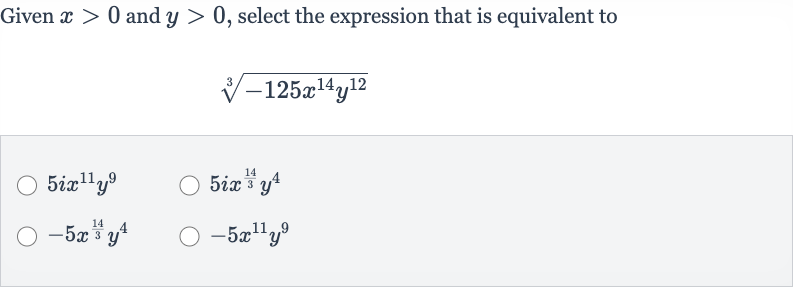Full solution
Q. Given and , select the expression that is equivalent to
- Evaluate Constant Term Cube Root: Evaluate the cube root of the constant term.The cube root of is because .
- Evaluate x Exponent Cube Root: Evaluate the cube root of .To find the cube root of , we divide the exponent by : .
- Evaluate y Exponent Cube Root: Evaluate the cube root of .To find the cube root of , we divide the exponent by : .
- Combine Results: Combine the results from Steps , , and .The expression equivalent to is .