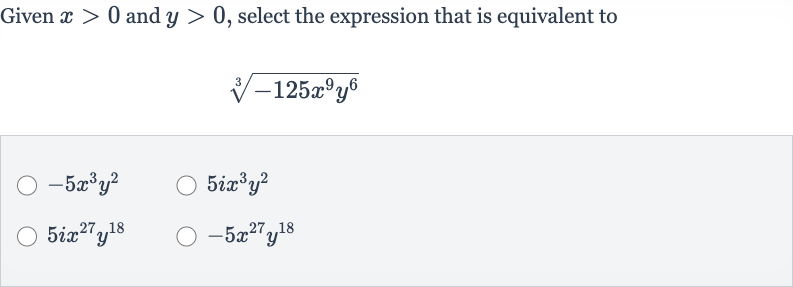Full solution
Q. Given and , select the expression that is equivalent to
- Identify cube root of product: Identify the cube root of a product. The cube root of a product is the product of the cube roots of each factor. So, .
- Calculate cube root of : Calculate the cube root of . The cube root of is because . .
- Calculate cube root of : Calculate the cube root of .The cube root of is because when you take the cube root, you divide the exponent by ..
- Calculate cube root of : Calculate the cube root of . The cube root of is because when you take the cube root, you divide the exponent by . .
- Combine results to find equivalent expression: Combine the results to find the equivalent expression.Combining the results from steps , , and , we get:.