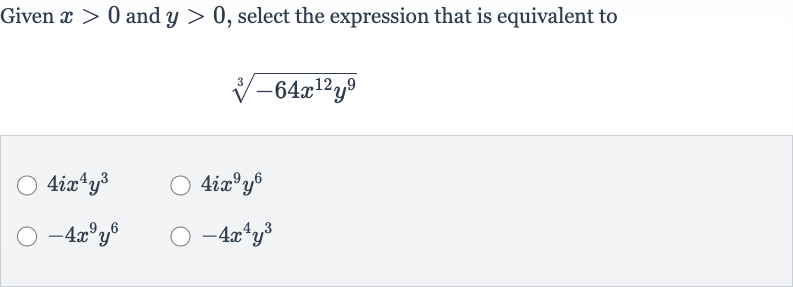Full solution
Q. Given and , select the expression that is equivalent to
- Simplify Constant Term: Simplify the cube root of the constant term.The cube root of is because .
- Simplify Variable Term : Simplify the cube root of the variable term . The cube root of is because when taking the cube root, you divide the exponent by . So, .
- Simplify Variable Term : Simplify the cube root of the variable term . The cube root of is because when taking the cube root, you divide the exponent by . So, .
- Combine Results: Combine the results from Steps , , and . Combining the cube roots of the constant and variable terms, we get .
- Check Given Options: Determine if the result is one of the given options.The result from Step is , which matches one of the given options.