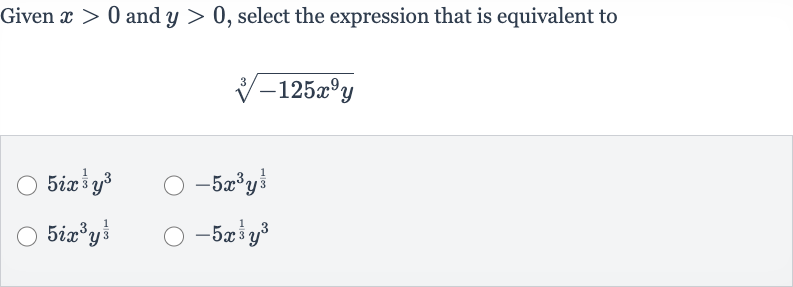Full solution
Q. Given and , select the expression that is equivalent to
- Simplify Constant: Simplify the constant inside the cube root.The cube root of is because .
- Simplify Variable : Simplify the variable inside the cube root. The cube root of is because .
- Simplify Variable : Simplify the variable inside the cube root. Since is not raised to a power that is a multiple of , it remains inside the cube root. Therefore, the cube root of is .
- Combine Simplified Parts: Combine the simplified parts.Combining the results from steps , , and , we get the expression .