Full solution
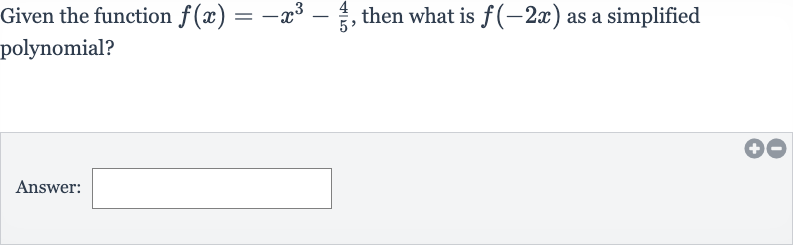
Q. Given the function , then what is as a simplified polynomial?Answer:
- Substitute into function: First, we need to substitute into the function .
- Calculate cube of : Now, we calculate the cube of .
- Substitute cube value back: Substitute the value of back into the function.
- Multiply negative sign: Multiply the negative sign into the cube of .
- Final simplified function: The function is now simplified and there are no further simplifications needed.