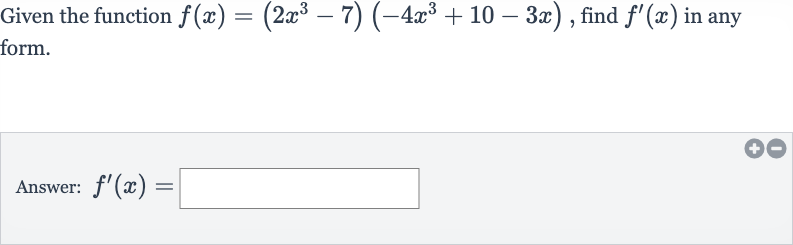
Given the function f(x)=(2x^(3)-7)(-4x^(3)+10-3x), find f^(')(x) in any form. Answer: f^(')(x)=

Question

Given the function  f(x)=(2x^(3)-7)(-4x^(3)+10-3x), find  f^(')(x) in any form. Answer:  f^(')(x)=

Bytelearn · Accepted Answer

Apply Product Rule: To find the derivative of the function f(x)=(2x^(3)-7)(-4x^(3)+10-3x), we will use the product rule. The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.Define Functions: Let's denote the first function as u(x) = 2x^3 - 7 and the second function as v(x) = -4x^3 + 10 - 3x. We will find the derivatives of u(x) and v(x) separately.Find u'(x): The derivative of u(x) = 2x^3 - 7 with respect to x is u'(x) = d/dx(2x^3) - d/dx(7). Using the power rule, we get u'(x) = 3*2x^(3-1) - 0 = 6x^2.Find v'(x): The derivative of v(x) = -4x^3 + 10 - 3x with respect to x is v'(x) = d/dx(-4x^3) + d/dx(10) - d/dx(3x). Using the power rule and the fact that the derivative of a constant is zero, we get v'(x) = -3*4x^(3-1) - 0 - 3 = -12x^2 - 3.Apply Product Rule Again: Now we apply the product rule: f'(x) = u'(x)v(x) + u(x)v'(x). Substituting the derivatives we found, we get f'(x) = (6x^2)(-4x^3 + 10 - 3x) + (2x^3 - 7)(-12x^2 - 3).Expand Terms: We will now expand the terms: f'(x) = (6x^2)(-4x^3) + (6x^2)(10) - (6x^2)(3x) + (2x^3)(-12x^2) - (2x^3)(3) - (7)(-12x^2) - (7)(-3).Simplify Terms: Simplifying the terms, we get f'(x) = -24x^5 + 60x^2 - 18x^3 - 24x^5 - 6x^3 + 84x^2 + 21.Combine Like Terms: Combining like terms, we get f'(x) = -48x^5 - 24x^3 + 144x^2 + 21.

Given the function $f(x)=\left(2 x^{3}-7\right)\left(-4 x^{3}+10-3 x\right)$ , find $f^{\prime}(x)$ in any form. $\newline$ Answer: $f^{\prime}(x)=$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Given the function f(x)=(2x3−7)(−4x3+10−3x) f(x)=\left(2 x^{3}-7\right)\left(-4 x^{3}+10-3 x\right) f(x)=(2x3−7)(−4x3+10−3x), find f′(x) f^{\prime}(x) f′(x) in any form.\newlineAnswer: f′(x)= f^{\prime}(x)= f′(x)=

Given the function $f(x)=\left(2 x^{3}-7\right)\left(-4 x^{3}+10-3 x\right)$ , find $f^{\prime}(x)$ in any form. $\newline$ Answer: $f^{\prime}(x)=$