Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Given that f(x)=x-1,quad g(x)=3x and h(x)=f(x-1)+3g(x-2), then what is the value of h(1) ? Answer:

Given that f(x)=x−1,g(x)=3x f(x)=x-1, \quad g(x)=3 x and h(x)=f(x−1)+3g(x−2) h(x)=f(x-1)+3 g(x-2) , then what is the value of h(1) h(1) ?\newlineAnswer:

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Solve multi-step linear equationsright chevron icon

Full solution

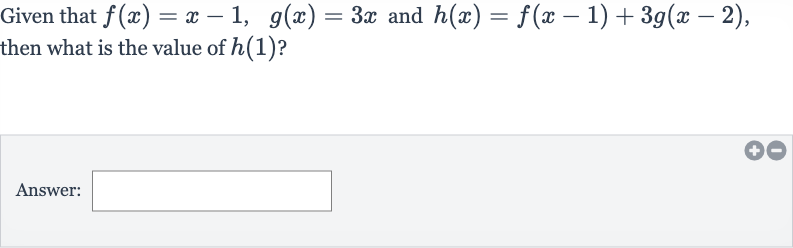
Q. Given that f(x)=x−1,g(x)=3x f(x)=x-1, \quad g(x)=3 x and h(x)=f(x−1)+3g(x−2) h(x)=f(x-1)+3 g(x-2) , then what is the value of h(1) h(1) ?\newlineAnswer:
  1. Find f(x−1)f(x-1) at x=1x=1: First, we need to find the value of f(x−1)f(x-1) when x=1x=1.
    f(x)=x−1f(x) = x - 1
    f(1−1)=f(0)=0−1=−1f(1 - 1) = f(0) = 0 - 1 = -1
  2. Calculate g(x−2)g(x-2) at x=1x=1: Next, we calculate the value of g(x−2)g(x-2) when x=1x=1.
    g(x)=3xg(x) = 3x
    g(1−2)=g(−1)=3(−1)=−3g(1 - 2) = g(-1) = 3(-1) = -3
  3. Find 3g(x−2)3g(x-2) at x=1x=1: Now, we need to find the value of 3g(x−2)3g(x-2) when x=1x=1. \newline3g(x−2)=3×g(−1)=3×(−3)=−93g(x-2) = 3 \times g(-1) = 3 \times (-3) = -9
  4. Find h(x)h(x) at x=1x=1: Finally, we can find the value of h(x)h(x) when x=1x=1.
    h(x)=f(x−1)+3g(x−2)h(x) = f(x-1) + 3g(x-2)
    h(1)=f(0)+3g(−1)=−1+(−9)=−10h(1) = f(0) + 3g(-1) = -1 + (-9) = -10

More problems from Solve multi-step linear equations

Question
Solve for x. \newline(34)x=12(\frac{3}{4})x= 12 \newlinex=x = ______
Get tutor helpright-arrow

Posted 1 year ago

Question
Solve for x. \newline−59x=15-\frac{5}{9}x= 15 \newlinex=x = ______
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline5x+8−7x=−4x+15x+8-7x=-4x+1\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−2z+10+7z=16z+7-2z+10+7z=16z+7\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline7(y−8)=7y+427(y-8)=7y+42\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−9(x+6)=−9x+108-9(x+6)=-9x+108\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−6(x+7)=−4x−2-6(x+7)=-4x-2\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−4x−7+10x=−7+6x-4x-7+10x=-7+6x\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline−17(y−2)=−17y+64-17(y-2)=-17y+64\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

Question
How many solutions does the following equation have?\newline9z−6+7z=16z−69z-6+7z=16z-6\newlineChoose 11 answer:\newline(A) No solutions\newline(B) Exactly one solution\newline(C) Infinitely many solutions
Get tutor helpright-arrow

Posted 1 year ago

View all (163)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant