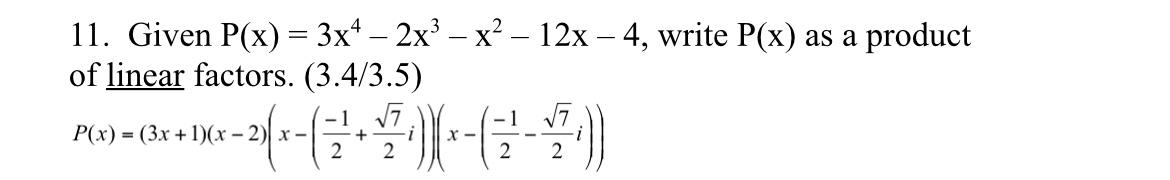
Given P(x)=3x^(4)-2x^(3)-x^(2)-12 x-4, write P(x) as a product of linear factors. (3.4/3.5) P(x)=(3x+1)(x-2)(x-((-1)/(2)+(sqrt7)/(2)i))(x-((-1)/(2)-(sqrt7)/(2)i))

Question

Given  P(x)=3x^(4)-2x^(3)-x^(2)-12 x-4, write  P(x) as a product of linear factors. (3.4/3.5)   P(x)=(3x+1)(x-2)(x-((-1)/(2)+(sqrt7)/(2)i))(x-((-1)/(2)-(sqrt7)/(2)i))

Bytelearn · Accepted Answer

Identify Possible Rational Roots: To factor the polynomial P(x)=3x^(4)-2x^(3)-x^(2)-12x-4, we first look for any rational roots using the Rational Root Theorem. The possible rational roots are the factors of the constant term (-4) divided by the factors of the leading coefficient (3).Test x=1: The factors of -4 are ±1, ±2, ±4, and the factors of 3 are ±1, ±3. So the possible rational roots are ±1, ±1/3, ±2, ±2/3, ±4, ±4/3. We can test these roots by direct substitution into the polynomial or by using synthetic division.Test x=-1: Let's test x=1: P(1)=3(1)^4-2(1)^3-(1)^2-12(1)-4 = 3-2-1-12-4 = -16, which is not zero. So x=1 is not a root.Test x=2: Let's test x=-1: P(-1)=3(-1)^4-2(-1)^3-(-1)^2-12(-1)-4 = 3+2-1+12-4 = 12, which is not zero. So x=-1 is not a root.Perform Polynomial Division: Let's test x=2: P(2)=3(2)^4-2(2)^3-(2)^2-12(2)-4 = 3*16-2*8-4-24-4 = 48-16-4-24-4 = 0. So x=2 is a root.Use Synthetic Division: Now that we have found a root, x=2, we can perform polynomial division or use synthetic division to divide P(x) by (x-2) to find the other factors.Factor the Cubic Polynomial: Using synthetic division with the root x=2, we divide P(x) by (x-2) and get a quotient of 3x^3+4x^2-9x-2.Test x=-1: We now need to factor the cubic polynomial 3x^3+4x^2-9x-2. We can again use the Rational Root Theorem to find possible rational roots for this cubic polynomial.Test x=-1/3: The possible rational roots for the cubic polynomial are the same as before: ±1, ±1/3, ±2, ±2/3, ±4, ±4/3. We test these roots by direct substitution or synthetic division.Test x=-1/3: Let's test x=-1: The cubic polynomial evaluated at x=-1 gives 3(-1)^3+4(-1)^2-9(-1)-2 = -3+4+9-2 = 8, which is not zero. So x=-1 is not a root.Let's test x=-1/3: The cubic polynomial evaluated at x=-1/3 gives 3(-1/3)^3+4(-1/3)^2-9(-1/3)-2 = -1/9+4/9+3-2 = 1/9+12/9-18/9 = -5/9, which is not zero. So x=-1/3 is not a root.Let's test x=-1/3 again, but this time more carefully. The cubic polynomial evaluated at x=-1/3 gives 3(-1/3)^3+4(-1/3)^2-9(-1/3)-2 = -1/9+4/9+3-2 = 3/9+27/9-18/9 = 12/9, which simplifies to 4/3. This is not zero, so x=-1/3 is indeed not a root.

Given $P(x)=3x^{4}-2x^{3}-x^{2}-12x-4$ , write $P(x)$ as a product of linear factors. ( $3$ . $4$ / $3$ . $5$ ) $\newline$ $P(x) = \left(3x + 1\right)\left(x - 2\right)\left(x - \left(-\frac{1}{2} + \frac{\sqrt{7}}{2}i\right)\right)\left(x - \left(-\frac{1}{2} - \frac{\sqrt{7}}{2}i\right)\right)$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics