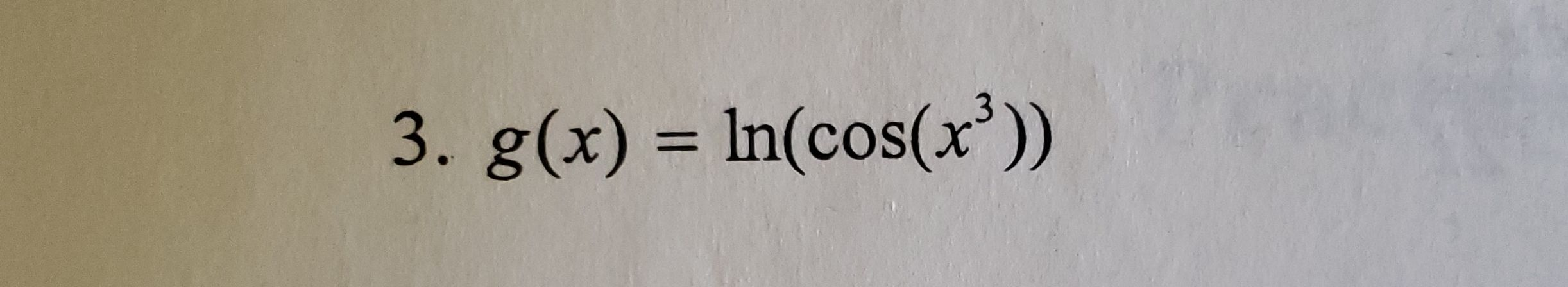AI tutor
Full solution
Q. .
- Identify Functions: To find the derivative of , we will use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
- Derivative of Outer Function: First, let's identify the outer function and the inner function. The outer function is , where is the inner function. In this case, the inner function is .
- Derivative of Inner Function: The derivative of the outer function with respect to is . So, when we take the derivative of , we will have times the derivative of the inner function .
- Combine Derivatives: Now, we need to find the derivative of the inner function . The derivative of with respect to is . Therefore, the derivative of with respect to is times the derivative of with respect to .
- Simplify Expression: The derivative of with respect to is . So, the derivative of with respect to is .
- Final Derivative: Putting it all together, the derivative of is the derivative of the outer function times the derivative of the inner function, which is .
- Final Derivative: Putting it all together, the derivative of is the derivative of the outer function times the derivative of the inner function, which is . Simplifying the expression, we get .
- Final Derivative: Putting it all together, the derivative of is the derivative of the outer function times the derivative of the inner function, which is .Simplifying the expression, we get .We can also express as , so the final simplified form of the derivative is .