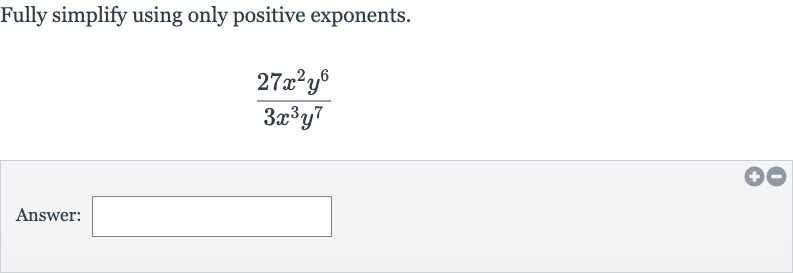Full solution
Q. Fully simplify using only positive exponents.Answer:
- Write Expression, Identify Like Terms: Write down the expression and identify like terms. We have powers of and in both the numerator and the denominator that can be simplified.
- Simplify Coefficients: Simplify the coefficients.Divide the coefficients by .
- Apply Quotient Rule for Exponents : Apply the quotient rule for exponents to .Since we want only positive exponents, we can rewrite as .
- Apply Quotient Rule for Exponents : Apply the quotient rule for exponents to .Similarly, we can rewrite as .
- Combine Results: Combine the results from steps , , and .
More problems from Simplify variable expressions using properties
QuestionGet tutor help