AI tutor
Full solution
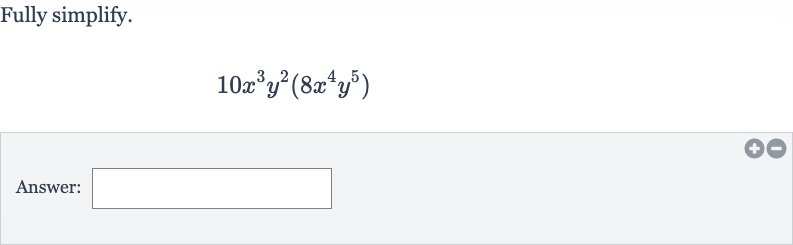
Q. Fully simplify.Answer:
- Multiply Coefficients and Apply Product Rule: To simplify the expression, we need to multiply the coefficients (numerical values) together and apply the product rule for exponents, which states that when multiplying like bases, we add the exponents.Calculation: Math error check: is indeed .
- Apply Product Rule to x Terms: Now we apply the product rule to the x terms. The product rule for exponents states that .Calculation: Math error check: Adding the exponents and correctly gives us .
- Apply Product Rule to Terms: Next, we apply the product rule to the terms in the same way.Calculation: Math error check: Adding the exponents and correctly gives us .
- Combine Results for Fully Simplified Expression: Finally, we combine the results from the previous steps to write the fully simplified expression.Calculation: Math error check: The coefficients and exponents have been correctly combined.