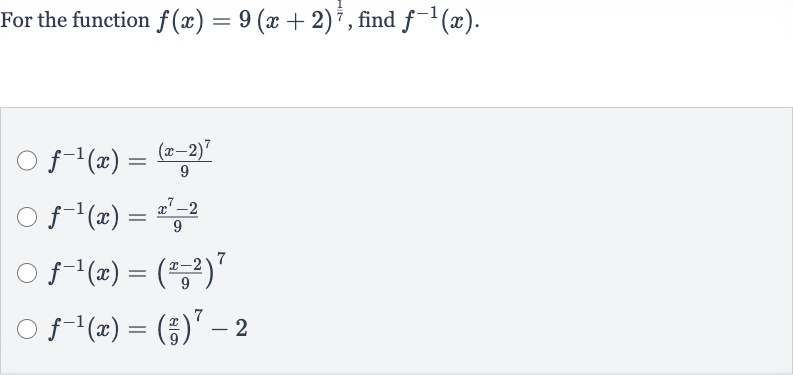AI tutor
Full solution
Q. For the function , find .
- Replace with : To find the inverse function, we start by replacing with for convenience:
- Swap x and y: Next, we swap x and y to begin solving for the new y, which will be the inverse function:
- Isolate y term: Now, we isolate the term containing y by dividing both sides by =
- Remove exponent: To remove the exponent, we raise both sides of the equation to the power of :
- Subtract : Subtract from both sides to solve for :
- Replace with : Finally, we replace with to denote the inverse function: