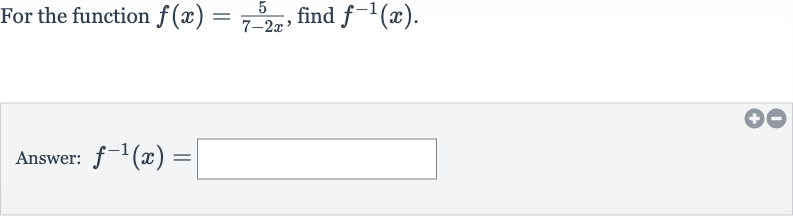
For the function f(x)=(5)/(7-2x), find f^(-1)(x). Answer: f^(-1)(x)=

Question

For the function  f(x)=(5)/(7-2x), find  f^(-1)(x). Answer:  f^(-1)(x)=

Bytelearn · Accepted Answer

Rewrite function with y: To find the inverse function, f^(-1)(x), we need to switch the roles of x and y in the original function and then solve for y. Let's start by rewriting the function with y instead of f(x): y = (5)/(7 - 2x)Switch x and y: Now, switch x and y to find the inverse: x = (5)/(7 - 2y)Multiply both sides: Next, we solve for y. Start by multiplying both sides of the equation by (7 - 2y) to get rid of the fraction: x * (7 - 2y) = 5Distribute x: Distribute x on the left side of the equation: 7x - 2xy = 5Isolate terms with y: Now, we want to isolate terms with y on one side. Let's move 7x to the right side by subtracting it from both sides: -2xy = 5 - 7xDivide by -2x: To solve for y, divide both sides by -2x (assuming x is not zero, as division by zero is undefined): y = (5 - 7x) / (-2x)Simplify the expression: We can simplify the expression by distributing the negative sign: y = (-5 + 7x) / (2x)Write as f^(-1)(x): This is the inverse function, so we can now write it as f^(-1)(x): f^(-1)(x) = (-5 + 7x) / (2x)

For the function $f(x)=\frac{5}{7-2 x}$ , find $f^{-1}(x)$ . $\newline$ Answer: $f^{-1}(x)=$

Full solution

More problems from Simplify variable expressions using properties

Related topics

For the function f(x)=57−2x f(x)=\frac{5}{7-2 x} f(x)=7−2x5​, find f−1(x) f^{-1}(x) f−1(x).\newlineAnswer: f−1(x)= f^{-1}(x)= f−1(x)=

For the function $f(x)=\frac{5}{7-2 x}$ , find $f^{-1}(x)$ . $\newline$ Answer: $f^{-1}(x)=$