AI tutor
Full solution
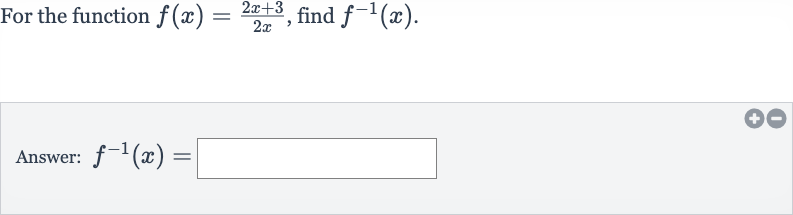
Q. For the function , find .Answer:
- Replace with : To find the inverse function, , we first replace with for easier manipulation.So, we have .
- Swap and : Next, we swap and to find the inverse. This gives us .
- Multiply by : Now, we solve for . To do this, we first multiply both sides by to get rid of the fraction:.
- Move terms: We then move all terms involving to one side and the constant to the other side: .
- Factor out : Factor out from the left side of the equation: .
- Divide by : Divide both sides by to solve for :
- Replace with : Replace with to denote that this is the inverse function:
More problems from Simplify variable expressions using properties
QuestionGet tutor help