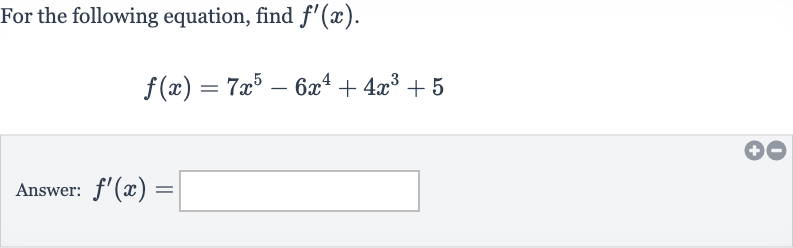
For the following equation, find f^(')(x). f(x)=7x^(5)-6x^(4)+4x^(3)+5 Answer: f^(')(x)=

Question

For the following equation, find  f^(')(x).  f(x)=7x^(5)-6x^(4)+4x^(3)+5 Answer:  f^(')(x)=

Bytelearn · Accepted Answer

Apply Power Rule: To find the derivative of the function f(x) = 7x^(5) - 6x^(4) + 4x^(3) + 5, we will apply the power rule to each term separately. The power rule states that the derivative of x^n with respect to x is n*x^(n-1).Derivative of 7x^(5): First, we find the derivative of the term 7x^(5). Using the power rule, we get: (d)/(dx)(7x^(5)) = 7 * 5 * x^(5-1) = 35x^(4).Derivative of -6x^(4): Next, we find the derivative of the term -6x^(4). Again, using the power rule, we get: (d)/(dx)(-6x^(4)) = -6 * 4 * x^(4-1) = -24x^(3).Derivative of 4x^(3): Then, we find the derivative of the term 4x^(3). Using the power rule, we get: (d)/(dx)(4x^(3)) = 4 * 3 * x^(3-1) = 12x^(2).Derivative of constant: Finally, the derivative of a constant is zero, so the derivative of the term +5 is: (d)/(dx)(5) = 0.Combine all derivatives: Now, we combine the derivatives of all the terms to find the derivative of the entire function f(x): f^(')(x) = 35x^(4) - 24x^(3) + 12x^(2) + 0.

For the following equation, find $f^{\prime}(x)$ . $\newline$ $f(x)=7 x^{5}-6 x^{4}+4 x^{3}+5$ $\newline$ Answer: $f^{\prime}(x)=$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

For the following equation, find f′(x) f^{\prime}(x) f′(x).\newlinef(x)=7x5−6x4+4x3+5 f(x)=7 x^{5}-6 x^{4}+4 x^{3}+5 f(x)=7x5−6x4+4x3+5\newlineAnswer: f′(x)= f^{\prime}(x)= f′(x)=

For the following equation, find $f^{\prime}(x)$ . $\newline$ $f(x)=7 x^{5}-6 x^{4}+4 x^{3}+5$ $\newline$ Answer: $f^{\prime}(x)=$