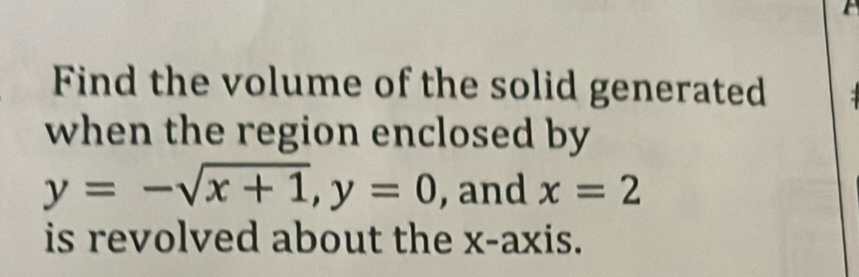Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the volume of the solid generated when the region enclosed by
y=-sqrt(x+1),y=0, and
x=2 is revolved about the
x-axis.

Find the volume of the solid generated when the region enclosed by $y=-\sqrt{x+1}, y=0$ , and $x=2$ is revolved about the $\mathrm{x}$ -axis.

View step-by-step help

View step-by-step help

Find derivatives of sine and cosine functions

Full solution

Q. Find the volume of the solid generated when the region enclosed by

y=-\sqrt{x+1}, y=0

, and

x=2

is revolved about the

\mathrm{x}

-axis.

Identify Curves and Limits: Identify the curves and limits for integration. $\newline$ The region is bounded by $y = -\sqrt{x+1}$ , $y = 0$ , and $x = 2$ . The solid is revolved around the $x$ -axis, so we use the disk method.
Set Up Integral for Volume: Set up the integral for the volume. $\newline$ The volume $V$ of the solid of revolution is given by the integral of $\pi$ times the square of the radius of the disks. The radius here is the y-value, which is $-\sqrt{x+1}$ , and the limits of integration are from $x = -1$ to $x = 2$ . $\newline$ $V = \pi \int_{x=-1}^{x=2} (-\sqrt{x+1})^2 \, dx$

More problems from Find derivatives of sine and cosine functions

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago