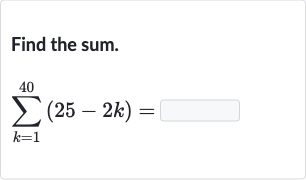AI tutor
Full solution
Q. Find the sum.
- Find Arithmetic Series Sum: We need to find the sum of the arithmetic series where the first term is , the common difference is , and the number of terms is .
- Use Sum Formula: To find the sum of an arithmetic series, we use the formula , where is the sum of the first terms, is the first term, and is the th term.
- Calculate th Term: First, we need to find the th term, . Since the common difference is , we can calculate as .
- Find : Calculating gives us .
- Plug Values into Formula: Now we have and . We can plug these values into the sum formula: .
- Simplify Sum Formula: Simplifying the sum formula gives us .
- Calculate Final Sum: Calculating gives us .
More problems from Negative Exponents
QuestionGet tutor help