Find the sum of the first $9$ terms of the following series, to the nearest integer. $\newline$ $6,2, \frac{2}{3}, \ldots$ $\newline$ Answer:

Full solution

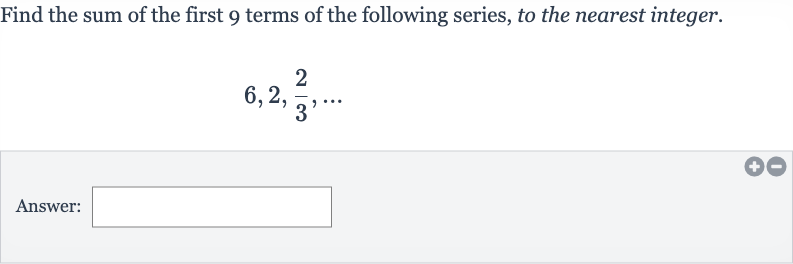
Q. Find the sum of the first

9

terms of the following series, to the nearest integer.

\newline

6,2, \frac{2}{3}, \ldots

\newline

Answer:

Identify Terms and Difference: The given series is an arithmetic series where each term decreases by a constant difference. To find the sum of the first $9$ terms, we need to identify the first term ( $a_1$ ), the common difference ( $d$ ), and the number of terms ( $n$ ). $\newline$ First term ( $a_1$ ) = $6$ $\newline$ Second term ( $a_2$ ) = $2$ $\newline$ Common difference ( $d$ ) = $a_2 - a_1 = 2 - 6 = -4$ $\newline$ Number of terms ( $n$ ) = $9$
Apply Sum Formula: The sum of the first $n$ terms of an arithmetic series can be found using the formula: $S_n = \frac{n}{2} \times (2a_1 + (n - 1)d)$ . Let's apply this formula to our series. $\newline$ $S_9 = \frac{9}{2} \times (2\times6 + (9 - 1)(-4))$
Calculate Sum: Now, let's calculate the sum using the values we have. $\newline$ $S_9 = \frac{9}{2} \times (12 + 8 \times (-4))$ $\newline$ $S_9 = \frac{9}{2} \times (12 - 32)$ $\newline$ $S_9 = \frac{9}{2} \times (-20)$
Simplify and Round: Simplifying the expression gives us the sum of the first $9$ terms. $S_9 = \frac{9}{2} \times (-20)$ $S_9 = -90$ Since we need to round to the nearest integer, the sum is already an integer, so no rounding is necessary.