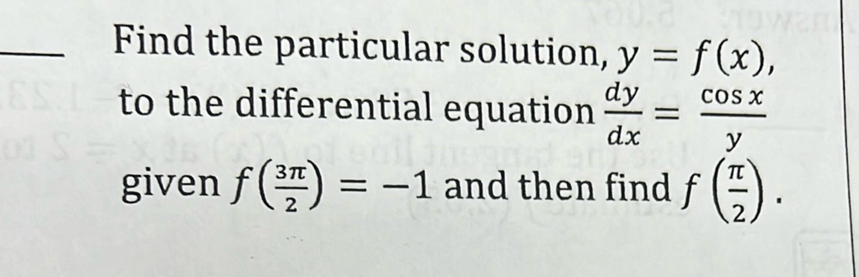Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Find the particular solution,
y=f(x), to the differential equation
(dy)/(dx)=(cos x)/(y) given
f((3pi)/(2))=-1 and then find
f((pi)/(2)).

Find the particular solution, $y=f(x)$ , to the differential equation $\frac{d y}{d x}=\frac{\cos x}{y}$ given $f\left(\frac{3 \pi}{2}\right)=-1$ and then find $f\left(\frac{\pi}{2}\right)$ .

View step-by-step help

View step-by-step help

Find derivatives of logarithmic functions

Full solution

Q. Find the particular solution,

y=f(x)

, to the differential equation

\frac{d y}{d x}=\frac{\cos x}{y}

given

f\left(\frac{3 \pi}{2}\right)=-1

and then find

f\left(\frac{\pi}{2}\right)

.

Separate and Integrate: Step $1$ : Separate variables and integrate. $\newline$ We start by separating the variables in the differential equation $\frac{dy}{dx} = \frac{\cos x}{y}$ . Rearrange to get $y dy = \cos x dx$ . $\newline$ Integrate both sides: $\newline$ $\int y dy = \int \cos x dx$ , $\newline$ $\frac{y^2}{2} = \sin x + C$ ,
Solve for y: Step $2$ : Solve for y. $\newline$ To find y, rearrange the equation: $\newline$ $y^2 = 2(\sin x + C)$ , $\newline$ $y = \pm\sqrt{2(\sin x + C)}$ ,
Find C: Step $3$ : Use the initial condition to find C. $\newline$ Given $f\left(\frac{3\pi}{2}\right) = -1$ , plug in $x = \frac{3\pi}{2}$ and $y = -1$ : $\newline$ $(-1)^2 = 2(\sin\left(\frac{3\pi}{2}\right) + C)$ , $\newline$ $1 = 2(-1 + C)$ , $\newline$ $1 = -2 + 2C$ , $\newline$ $2C = 3$ , $\newline$ $C = \frac{3}{2}$ ,
Write Solution: Step $4$ : Write the particular solution. $\newline$ With $C = \frac{3}{2}$ , the solution becomes: $\newline$ $y = \pm\sqrt{2(\sin x + \frac{3}{2})}$ , $\newline$ Since $f\left(\frac{3\pi}{2}\right) = -1$ , we choose the negative branch: $\newline$ $y = -\sqrt{2(\sin x + \frac{3}{2})}$ ,
Find $f(\frac{\pi}{2})$ : Step $5$ : Find $f\left(\frac{\pi}{2}\right)$ . $\newline$ Plug in $x = \frac{\pi}{2}$ : $\newline$ $f\left(\frac{\pi}{2}\right) = -\sqrt{2(\sin\left(\frac{\pi}{2}\right) + \frac{3}{2})}$ , $\newline$ $f\left(\frac{\pi}{2}\right) = -\sqrt{2(1 + \frac{3}{2})}$ , $\newline$ $f\left(\frac{\pi}{2}\right) = -\sqrt{2 \times 2.5}$ , $\newline$ $f\left(\frac{\pi}{2}\right) = -\sqrt{5}$ ,

More problems from Find derivatives of logarithmic functions

Question

Find the derivative of

f(x)

\newline

f(x) = \cos(x)

\newline

f'(x) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \ln(x)

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \tan^{-1}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = x e^x

\newline

f'\left(x\right) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = \frac{e^x}{x}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

f(x)

\newline

f(x) = e^{(x + 1)}

\newline

f'\left(x\right) =

Posted 1 month ago

Question

Find the derivative of

f(x)

\newline

f(x) = \sqrt{x+3}

\newline

f'(x) =

Posted 2 months ago

Question

Find the derivative of

g(x)

\newline

g(x) = \ln(2x)

\newline

g^{\prime}(x) =

Posted 3 months ago