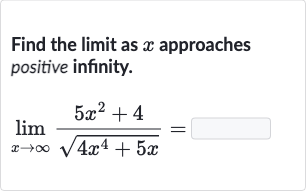Find the limit as x approaches positive infinity. lim_(x rarr oo)(5x^(2)+4)/(sqrt(4x^(4)+5x))=

Question

Find the limit as  x approaches positive infinity.  lim_(x rarr oo)(5x^(2)+4)/(sqrt(4x^(4)+5x))=

Bytelearn · Accepted Answer

Simplifying the expression: To find the limit of the given function as x approaches positive infinity, we need to analyze the behavior of the numerator and the denominator separately. We will start by simplifying the expression by dividing both the numerator and the denominator by the highest power of x in the denominator, which is x^2.Removing terms as x approaches infinity: Divide the numerator and the denominator by x^2: lim_(x rarr oo) (5x^2/x^2 + 4/x^2) / (sqrt(4x^4/x^2 + 5x/x^2)) Simplify the expression: lim_(x rarr oo) (5 + 4/x^2) / (sqrt(4x^2 + 5/x))Simplifying the square root: As x approaches positive infinity, the terms 4/x^2 and 5/x in the expression will approach zero. Therefore, we can simplify the expression further by removing these terms: lim_(x rarr oo) (5 + 0) / (sqrt(4x^2 + 0)) This simplifies to: lim_(x rarr oo) 5 / (sqrt(4x^2))Final step: approaching zero: Now, we can simplify the square root in the denominator: sqrt(4x^2) = 2x (since x is approaching positive infinity, we consider only the positive square root). So the expression becomes: lim_(x rarr oo) 5 / (2x)As x approaches positive infinity, the term 2x in the denominator will also approach infinity, making the whole fraction approach zero: lim_(x rarr oo) 5 / (2x) = 0

Find the limit as $x$ approaches positive infinity. $\newline$ $\lim _{x \rightarrow \infty} \frac{5 x^{2}+4}{\sqrt{4 x^{4}+5 x}}=$

Full solution

More problems from Powers with decimal and fractional bases

Related topics

Find the limit as x x x approaches positive infinity.\newlinelim⁡x→∞5x2+44x4+5x= \lim _{x \rightarrow \infty} \frac{5 x^{2}+4}{\sqrt{4 x^{4}+5 x}}= x→∞lim​4x4+5x​5x2+4​=

Find the limit as $x$ approaches positive infinity. $\newline$ $\lim _{x \rightarrow \infty} \frac{5 x^{2}+4}{\sqrt{4 x^{4}+5 x}}=$