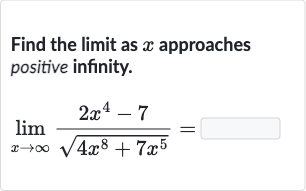AI tutor
Full solution
Q. Find the limit as approaches positive infinity.
- Identify highest power of : Identify the highest power of in the numerator and the denominator.In the numerator, the highest power of is . In the denominator, after taking the square root, the highest power of is (since ).
- Divide numerator and denominator: Divide the numerator and the denominator by , the highest power of found in the previous step.
- Simplify expression: Simplify the expression by canceling out the terms where possible.
- Approach positive infinity: As approaches positive infinity, the terms with in the denominator approach zero.
- Calculate simplified expression: Calculate the simplified expression.