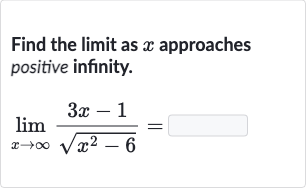AI tutor
Full solution
Q. Find the limit as approaches positive infinity.
- Understand the problem: Understand the problem.We need to find the limit of the function as approaches positive infinity. This involves understanding the behavior of the function as the value of gets larger and larger.
- Simplify the expression: Simplify the expression by dividing numerator and denominator by . To make it easier to find the limit, we divide both the numerator and the denominator by , the highest power of in the denominator.
- Evaluate the limit: Evaluate the limit of the simplified expression as approaches positive infinity.As approaches positive infinity, the terms and approach . Therefore, the expression simplifies to:
- Conclude the solution: Conclude the solution.The limit of the function as approaches positive infinity is .