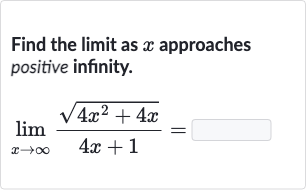Find the limit as x approaches positive infinity. lim_(x rarr oo)(sqrt(4x^(2)+4x))/(4x+1)=

Question

Find the limit as  x approaches positive infinity.  lim_(x rarr oo)(sqrt(4x^(2)+4x))/(4x+1)=

Bytelearn · Accepted Answer

Identify highest power of x: Identify the highest power of x in the numerator and denominator. In the expression (sqrt(4x^2+4x))/(4x+1), the highest power of x in the numerator inside the square root is x^2, and the highest power of x in the denominator is x.Divide numerator and denominator: Divide the numerator and the denominator by the highest power of x in the denominator. To simplify the limit, we divide both the numerator and the denominator by x. This gives us the expression (sqrt(4 + 4/x))/(4 + 1/x).Take limit as x approaches infinity: Take the limit as x approaches positive infinity. As x approaches positive infinity, the terms 4/x and 1/x in the expression (sqrt(4 + 4/x))/(4 + 1/x) approach 0. This simplifies the expression to (sqrt(4 + 0))/(4 + 0), which is (sqrt(4))/4.Simplify the expression: Simplify the expression. The square root of 4 is 2, so the expression (sqrt(4))/4 simplifies to 2/4, which can be further simplified to 1/2.State the final answer: State the final answer. The limit of (sqrt(4x^2+4x))/(4x+1) as x approaches positive infinity is 1/2.

Find the limit as $x$ approaches positive infinity. $\newline$ $\lim _{x \rightarrow \infty} \frac{\sqrt{4 x^{2}+4 x}}{4 x+1}=$

Full solution

More problems from Powers with decimal and fractional bases

Related topics

Find the limit as x x x approaches positive infinity.\newlinelim⁡x→∞4x2+4x4x+1= \lim _{x \rightarrow \infty} \frac{\sqrt{4 x^{2}+4 x}}{4 x+1}= x→∞lim​4x+14x2+4x​​=

Find the limit as $x$ approaches positive infinity. $\newline$ $\lim _{x \rightarrow \infty} \frac{\sqrt{4 x^{2}+4 x}}{4 x+1}=$